PHYsics
1151
Homework
Chapter 11: Fluids in
Motion
Ch 11: 1, 6, 7, 11,20, 22,
37
11.1 Water flows through a pipe at the rate of 0.35 m3/min. What is its speed where the pipe has a diameter of 1.5 cm? Where the diameter is 2.5 cm?
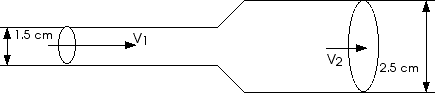
m/t=
A v = constant
=
1000 kg/m3
Since the density remains constant, we can just concentrate on the volume flow rate (VFR) which is 0.35 m3/min. While it is fine to leave it in units of m3/min, I simply feel more "comfortable" converting the time unit to seconds
V/t
= 0.35 m3/min [min/60
sec] = 0.0058 m3/s
V/t
= 0.0058 m3/s [100 cm/m]3 = 5,833
cm3/s
A1 = 
r12 = ¹ (0.75 cm)2 = 1.77
cm2
A2 =
r22 = ¹ (1.25 cm)2 = 4.91
cm2
V/t
= A v
Be careful. I am using capital V for volume and small v for velocity (or speed).
V/t
= A v = A1 v1 = A2 v2
v = [V/t]
/A
v1 = [V/t]
/A1
v1 = [5,833 cm3/s] /1.77 cm2
v1 = 3,296 cm/s = 33 m/s
v = [V/t]
/A
v2 = [V/t]
/A2
v2 = [5,833 cm3/s] /4.91 cm2
v2 = 1,188 cm/s = 12 m/s
Be very careful of the units!
11.6 What must be the gauge pressure at a fire hydrant if water from a fire hose is to reach a height of 12 m?
We can immediately apply Bernoulii’s Equation,
v2 +
g h + p = constantor
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p2In our case, the hydrant is position 1 and the top of the stream of water is position 2,
h1 = 0
p1 = p1g = ?
and
h2 = 12 m
p2 = p2g = 0
(the guage pressure at the top of the stream is zero).
(0)2 +
g (0) + p1g = 1/2
(0)2 +
g (12 m) + (0)p1g =
g (12 m)p1g = (1000 kg/m3) (9.8 m/s2) (12 m)
p1g = 117,600 N/m3 = 117,600 Pa = 117.6 kPa
p1g = 117.6 kPa
p1g = 117.6 kPa [1 atm / 101.3 kPa] = 1.16 atm
Remember, the subscript "g" simply means "gauge pressure".
11.7 Air (r = 1.3 kg/m3) blows past a 1.0 m x 2.5 m window with a speed of 20 m/s. What is the difference in pressure on the two sides of the window? What is the net force on the window?
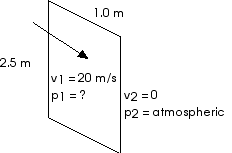
We can (again) immediately apply Bernoulii’s Equation,
v2 +
g h + p = constantor
v12
+
g h1 + p1 = 1/2
v22 +
g h2 + p2In our case, position 1 is outside the window and position 2 is inside the window. The height is the same so
1/2
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p21/2
(20 m/s)2 +
g h + p1 = 1/2
(0)2 +
g h + p21/2
(20 m/s)2 + [g
h] + p1 = 1/2
(0)2 + [
g h] + p21/2
(20 m/s)2 = p2 - p1p2 - p1 = 1/2
(20 m/s)2 = 1/2 (1.3
kg/m3) (20 m/s)2 = 260 N/m2 = 260
Pap
= 260 PaF =
p
A = (260 N/m2)(1.0 m x 2.5 m) = 650 NF = 650 N
11.11 Below are data for the cross-sectional area of open
pipes and the pressure head behind each. (The “pressure
head” is the gauge pressure measured in meters of
water). Find the volume flow rate through each pipe.
cross-section area pressure head pipe (cm2) ( m ) a 1.0 2.5 b 1.2 2.5 c 1.5 3.5 d 1.8 3.0 e 3.0 4.0 f 3.0 5.0 g 5.0 6.0
This will be a good problem to solve once algebraicly and then
use a spreadsheet to solve for each particular set of numbers.
We begin, again, with Bernoulii’s Equation,
v2 +
g h + p = constantor
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p2We are not concerned with any difference in height, so we may set h1 = h2 = h. Then our equation becomes
v12 + p1 =
1/2
v22 + p2We can think of the flow rate due to a pressure difference as
the flow out of a large tank. Inside the tank the flow velocity is
essentially zero. A diagram may help --
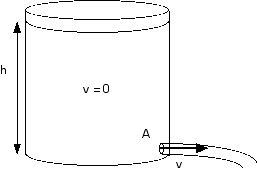
1/2
v12 + p1 =
1/2
v22 + p21/2
(0)2 + p1 = 1/2
v22 + p2p1 - p2 = 1/2
v221/2
v22 = p1 - p21/2
v22 =
pHowever, this difference in pressure is often refered to as a “pressure head” and is then stated in terms of the height of a column of water that would provide this difference in pressure; that is
p = g
h1/2
v22 =
p1/2
v22 =
g h1/2 v22 = g h
v22 = 2 g h
(This is also known as Torecelli’s Theorem).
Now that we know the velocity, the volume flow rate is just the
velocity multiplied by the cross-sectional area,
Now we are ready to create a spreadsheet to do the actual calculations. However, a word of caution is appropriate here. Be careful with the units!
c-s area
c-s area
press head
vol flow rate
cm*cm
m*m
m
m^3/s
a
1.00
0.00010
2.50
0.00070
b
1.20
0.00012
2.50
0.00084
c
1.50
0.00015
2.50
0.00105
d
1.80
0.00018
3.00
0.00138
e
3.00
0.00030
4.00
0.00266
f
3.00
0.00030
5.00
0.00297
g
5.00
0.00050
6.00
0.00542
As an example, the formula for pipe a, which appears in cell
E3, is
11.20 The inside diameter of the larger part of the pipe in Figure 11.22 is 2.50 cm. Water flows through the pipe at a rate of 1.80 l/s. What is the inside diameter of the constriction?
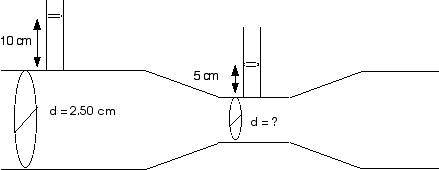
A better diagram might look more like this-
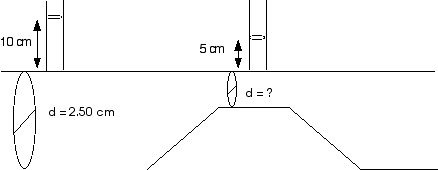
We begin, again, with Bernoulii’s Equation,
v2 +
g h + p = constantor
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p2We are not concerned with any difference in height, so we may set h1 = h2 = h. Then our equation becomes
v12 + p1 =
1/2
v22 + p2We know the volume flow rate of 0.180 l/s. In the larger part of the pipe, we know the cross-section area A1,
volume flow rate = Av = A1 v1
v1 = [volume flow rate]/A1 =
[0.180 x 10-3 m3/s]/[ 4.91 x
10-4 m2]
v1 = 0.367 m/s
where we have made use of
1/2
v12 + p1 =
1/2
v22 + p21/2
(0.367 m/s)2 + p1 - p2 =
1/2
v221/2
v22 = 1/2
(0.367 m/s)2 + p1 - p2v22 = (0.367 m/s)2 + 2 (p1 - p2)/r
We know the pressures p1 and p2 in terms of the “pressure head”, the height of the column of water that is equivalent to these pressures.
g hp1 =
g h1 = (1000 kg/m3) (9.8
m/s2) ( 0.10 m)p2 =
g h2 = (1000 kg/m3) (9.8
m/s2) ( 0.05 m)p2 - p1 =
g h2 -
g h12 (p1 - p2)/
=
2 (
g h2 -
g h1)/
= g (h2 - h1) = (9.8 m/s2)(0.05
m) = 0.49 m2/s2
v22 = (0.367 m/s)2 + 2
(p1 - p2)/r
v22 = (0.367 m/s)2 + 0.49
m2/s2
v22 = 0.13 m2/s2 +
0.49 m2/s2
v22 = 0.13 m2/s2 +
0.49 m2/s2
v22 = 0.62
m2/s2
v2 = 0.79 m/s
This is the velocity through the constriction. What area (or diameter) will provide this velocity?
A2 = [volume flow rate]/v2 =
A2 = [0.180 x 10-3 m3/s]/[0.79 m/s] =
A2 = 2.28 x 10-4 m2 = ¹ r2
r2 = 7.25 x 10-5 m2
r = 8.5 x 10-3 m
d = 2 r = 1.70 x 10-2 m
d = 1.7 cm
( finally! )
11.22 The dimensions given in Figure 11.24 are all inside diameters. When the faucet valve is wide open, it does not constrict the smaller pipe. If water enters the larger pipe under a pressure of 3800 torr, what volume emerges from the faucet per second. Compare this exact result with the restult obtained by disregarding the speed of the water in the larger pipe. Assume the pressure in the open faucet is 760 torr (1 atm).
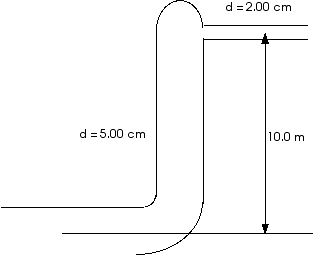
In the large pipe, at position 1,
h1 = 0
A1 = ¹ r12 = ¹ (0.0025 m)2 = 1.96 x 10-5 m2
In the small pipe, at position 2,
h2 = 10 m
A2 = ¹ r22 = ¹ (0.001 m)2 = 3.14 x 10-6 m2
As always, it would seem, we shall apply Bernoulii’s Equation,
v2 + r g h + p = constantor
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p2
VFR = volume flow rate = A1 v1 =
A2 v2
v1 = VFR/A1; v12 =
[VFR/A1]2
v2 = VFR/A2; v22
= [VFR/A2]2
Now we know everything in Bernoulii’s Equation, except the volume flow rate (VFR) so we can (finally) solve for that!
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p21/2
[VFR/A1]2 +
g h1 + p1 = 1/2
[VFR/A2]2 +
g h2 + p2[VFR/A1]2 + 2 g h1 + 2 p1/
= [VFR/A2]2 + 2 g h2 + 2
p2/[VFR/A1]2 - [VFR/A2]2 = 2 g (h2 - h1) + 2 (p2 - p1)/
VFR2 [ (1/A1)2 - (1/A2)2 ] = 2 g (h2 - h1) + 2 (p2 - p1)/
VFR2 [(A22 - A12)/(A12 A22)] = 2 g (h2 - h1) + 2 (p2 - p1)/
VFR2 = [ 2 g (h2 - h1) + 2 (p2 - p1)/
]
[(A12
A22)/(A22 -
A12)]Now (finally!) we can plug
in numbers,
VFR2 = [2 (9.8 m/s2) (10 m - 0) + 2 (-
404,000 N/m2)/(1000 kg/m3)] x
x [(( 3.14 x 10-6 m2)2 (1.96 x 10-5 m2)2)/(( 3.14 x 10-6 m2)2 - (1.96 x 10-5 m2))2)]
(messy, eh? Sure, but fairly straightforward, nonetheless).
VFR2 = [196 m2/s2 - 808 m2/s] [(3.79 x 10-21 m8)/(- 374 x 10-12 m4)]
VFR2 = [ - 612 m2/s2 ] [ - 1.01 x 10-11 m4 ]
VFR2 =6.202 x 10-9 m6/s2
VFR = 7.88 x 10-5 m3/s
VFR = 7.88 x 10-5 m3/s [ 1000 l/s ] =0.0788 l/s (liters per second)
Regard the larger pipe as a large tank with v1 = 0. Then Bernoulii’s Equation is
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p20 +
g h1 + p1 = 1/2
v22 +
g h2 + p21/2
v22 + r g h2 + p2 =
g h1 + p11/2
v22 = g
(h1 - h2) + (p1 -
p2)v22 = 2 g (h1 - h2) + 2 (p1 - p2)/
v22 = 2 (9.8 m/s2) (0 - 10 m) + 2 (505 kPa - 101 kPa)/(1000 kg/m3)
v22 = - 196 m2/s2 +808 m2/s2
v22 = 612 m2/s2
v2 = 24.7 m/s
This number seems large, but believable. Now, what is the volume flow rate?
VFR = 7.77 x 10-5 m3/s [ 1000 l/m3 ] = 0.077 l/s (liters per second)
And that seems like a reasonable number. The answers in
the two cases are very similar so treating the larger pipe as a
large tank is a very reasonable approximation.
Be sure to check on units!
11.37 The heart of a person sitting quietly pumps blood at the rate of 4 x 103 cm3/min through an aorta of cross section 0.8 cm2.
a) What is the average blood speed in the aorta?
The blood then spreads out into a network of about 5 x 109 (!) tiny capillaries whose average radius is about 8 x 10-4 cm.
b) What is the speed of the blood through these capillaries?
v = VFR/A = [4 x 103 cm3/min] / [0.8 cm2] = 5,000 cm/min = 50 m/min
v = 50 m/min [min/60 s] = 0.83 m/s
What is the total area of the capillaries?
While each capillary has a very small cross section, there are five billion of them!
VFR = volume flow rate = A v
v = VFR/A = [4 x 103 cm3/min] / [1.00 x 104 cm2] = 4 x 10-1 cm/min
v = 0.4 cm/min [min/60 s] = 6.67 x 10-3 cm/s
As you should expect, that velocity is very slow because the total cross section area is very large.
(c) 2000, Doug Davis; all rights reserved