Chapter 8; Static Equilibrium
8.3, 10, 22, 29, 52, 55, 56, 74

| ToC, Ch 8 | Course Calendar|

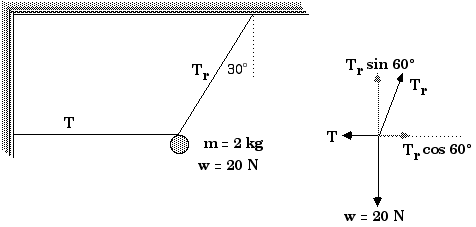
8.3 A 2-kg ball is held in position by a horizontal string and a string that makes an angle of 30° with the vertical, as shown in the figure. Find the tension T in the horizontal string.

F = 0

(Since I am writing this all in bold to begin with, it is difficult or impossible to explicitly tell that this is a vector equation--but it is! And that's very important!)

F = 0

But that really means

Fx = 0
and
Fy = 0
Fx = - T + Tr cos 60° = 0

Fy = Tr sin 60° - 20 N = 0
- T + Tr (0.500) = 0

Tr (0.866) - 20 N = 0
T = Tr (0.500)

Tr (0.866) = 20 N

Tr =

Tr = 23.1 N

T = (23.1 N)(0.500)

T = 11.5 N

8.10 The pulleys shown in the figure below are frictionless but have a mass of 4 kg each. What is the tension in the cord and in the pulley supports?


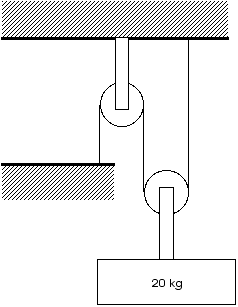
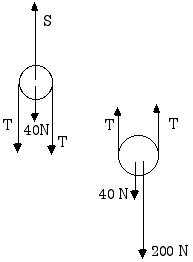
Apply the first condition of equilibrium to each pulley.
First to the one one the left,

F = 0
F = S - T - 40 N - T = 0
S - 2 T = 40 N

That gives two unknowns in one equation so we must seek additional information. Of course, that will come from looking at the pulley on the right,

F = 0
F = 2 T - 40 N - 200 N = 0
2 T = 240 N
T = 120 N

S = 40 N + 2 T = 40 N + 2 (120 N)
S = 280 N

8.22 a cable and pulley arrangement shown there. The coefficient of friction between the two blocks is 0.4. The coefficient of friction between the block and the floor is 0.4. What is the maximum external horizontal force F that can be exerted on the lower block before it will move? What is the tension in the cable?


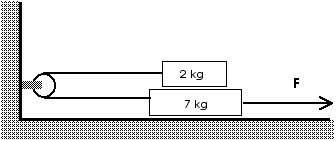
The maximum external force F that can be exerted will be the force exerted when the friction forces are at their maxima,

Ff = µ FN

Make careful free body diagrams of the forces on each block.
First, for the 2-kg block, we have


F = 0

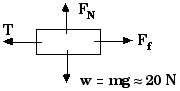
But that really means

Fx = 0
and
Fy = 0
Fx = Ff - T = 0

Fy = FN - 20 N = 0
Ff = T

FN = 20 N
With the normal force on the 2 kg block known, we can readily calculate the friction force,

Ff = (0.4) (20 N)
Ff = 8 N

And that also means

T = 8 N

Now, look at all the forces on the 7-kg block,

 

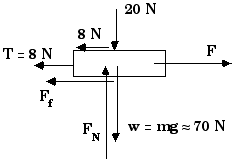
The downward 20 N-force on top of the block is the normal force exerted by the 2-kg block. The 8-N force on the top is the friction force exerted by the 2-kg block. The tension is still 8 N just as it was at the other end of the string which is attached to the 2-kg block. The forces labeled FN and Ff are the normal force and friction force exerted at the bottom on this 7-kg block, of course. We used the same symbols to represent different forces earlier when we looked at the 2-kg block. Now we are ready to again apply the first condition of equilibrium,

F = 0

But that really means

Fx = 0
and
Fy = 0
Fx = F - Ff - 8 N - 8 N = 0

Fy = FN - 20 N - 70 N = 0
F = Ff + 16 N

FN = 90 N

With the normal force on the 7-kg block known, we can readily calculate the friction force,

Ff = (0.4) (90 N)
Ff = 36 N
F = Ff + 16 N
F = 36 N + 16 N
F = 52 N

8.29 A piece of pipe may sometimes be used as a "cheater" to effectively lengthen the moment arm of a wrench. If a pipe is used as shown in the figure to allow a 150 N force to be exerted 30 cm from the bolt, what torque is exerted on the bolt?

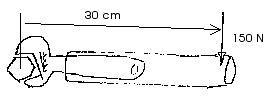
= r F sin
= (0.30 m) (150 N) (1)
= 45 m-N

8.35 (original) A uniform pole 6 m long weighs 300 N and is attached by a pivot at one end to a wall. The pole is held at an angle of 30° above the horizontal by a horizontal guy wire attached to the pole 4.0 m from the end attached to the wall. A load of 600 N hangs from the upper end of the pole. Find the tension in the guy wire and the components of the force exerted on the pole by the wall.

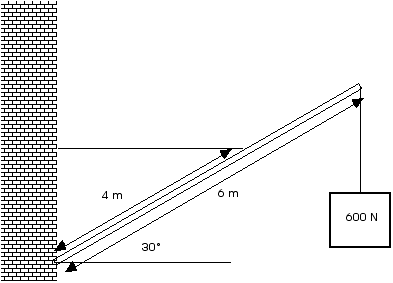
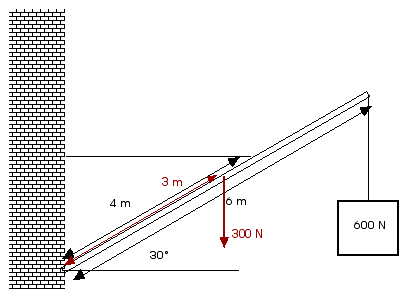
As always, a free body diagram is essential.


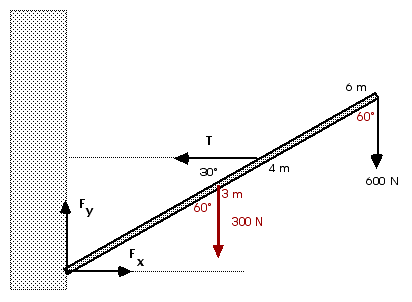
From the first condition of equilibrium, we have

F = 0

But that really means

Fx = 0
and
Fy = 0
Fx = Fx - T = 0

Fy = Fy - 600 N - 300 N = 0
Fx = T

Fy = 900 N

More information is needed to solve for T and Fx. We can get that information from the second condition of equilibrium. Before we start to calculate torques, we must decide on the reference point about which we will calculate those torques. If we choose the lower, left end of the pole, there are two forces, Fx and Fy, that will have zero torque. That will reduce the number of terms in all of our equations. Therefore, that is a good choice for the origin or reference point or axis of rotation.

List each force and the torque caused by that force:

Fx: = 0 (since r = 0 in = r F sin )
Fy: = 0 (since r = 0 in = r F sin )
T: ccw = (4 m)(T)(sin 30°) = (4 m) T (0.50) = (2 m) T
600 N: cw = (6 m)(600 N)(sin 60°) = (6 m)(600 N)(0.866) = 3118 m-N

300 N: cw = (3 m)(300 N)(sin 60°) = (3 m)(300 N)(0.866) = 779 m-N

ccw = cw
(2 m) T = 3118 m-N + 779 m-N
(2 m) T = 3897 N

T = (3897/2) N

T = 1948.5 N

Therefore,

Fx = T

Fx = 1948.5 N

And we already knew

Fy = 900 N

8.35 (modified) A lightweight, uniform pole is 6 m long and is attached by a pivot at one end to a wall. The pole is held at an angle of 30° above the horizontal by a horizontal guy wire attached to the pole 4.0 m from the end attached to the wall. A load of 600 N hangs from the upper end of the pole. Find the tension in the guy wire and the components of the force exerted on the pole by the wall.


As always, a free body diagram or a force diagram is essential.


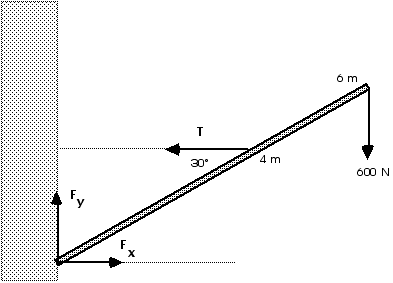
From the first condition of equilibrium, we have

F = 0

But that really means

Fx = 0
and
Fy = 0
Fx = Fx - T = 0

Fy = Fy - 600 N = 0
Fx = T

Fy = 600 N

More information is needed to solve for T and Fx. We can get that information from the second condition of equilibrium. Before we start to calculate torques, we must decide on the reference point about which we will calculate those torques. If we choose the lower, left end of the pole, there are two forces, Fx and Fy, that will have zero torque. That will reduce the number of terms in all of our equations. Therefore, that is a good choice for the origin or reference point or axis of rotation.

List each force and the torque caused by that force:

Fx: = 0 (since r = 0 in = r F sin )
Fy: = 0 (since r = 0 in = r F sin )
T: ccw = (4 m)(T)(sin 30°) = (4 m) T (0.50) = (2 m) T
600 N: cw = (6 m)(600 N)(sin 60°) = (6 m)(600 N)(0.866) = 3118 m-N

ccw = cw
(2 m) T = 3118 m-N
T = 1559 N

Therefore,

Fx = T

Fx = 1559 N

And we already knew

Fy = 600 N

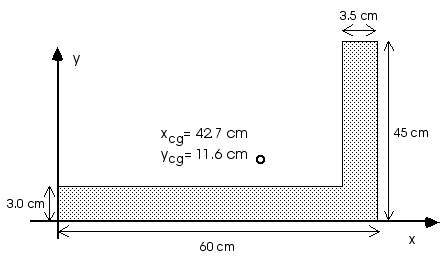
8.41 A carpenter's square has the dimensions shown in the figure. It is made of uniformly thick metal. Locate its center of gravity.

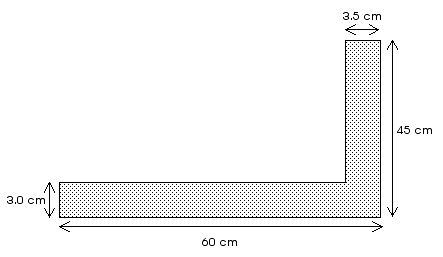
Think of the square as being made of two rectangles.

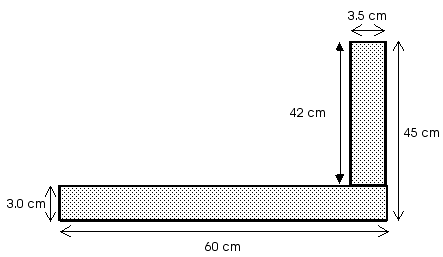
The center of gravity of each rectangle is at the geometric center of that rectangle and the mass (or weight) located at that position is proportional to the area of that rectangle.

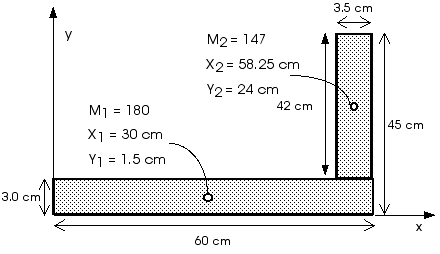
Notice that the positions are all measured from the lower left corner of the carpenter's square. Now we can use the defintions of center of gravity, Equations 8.10 and 8.11, to locate the center of gravity of the entire object,

8.52 Ladder problems are fun. Ladder problems are classic. A ladder problem will surely reappear on an hour exam or the final. A man who weighs 800 N climbs to the top of a 6 meter ladder that is leaning agains a smooth (ie, frictionless) wall at an angle of 60° with the horizontal as sketched in the figure below. The non-uniform ladder weighs 400 N and its center of gravity is 2 meters from the foot of the ladder. What must be the minimum coefficient of static friction between the ground and the foot of the ladder if it is not to slip?

 


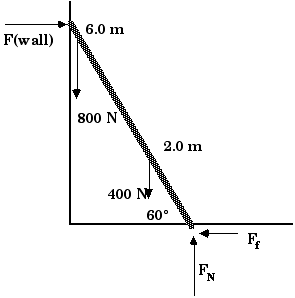
Using the first condition of equilibrium, we have

Fx = Fwall - Ff = 0

Fwall = Ff

and

Fy = FN - 400 N - 800 N = 0

FN = 1200 N

To solve for Fwall and, thus, for Ff, we must use the second condition of equilibrium. In calculating the torques, let us calculate torques about the foot of the ladder. That choice means two of the forces, FN and Ff , will provide zero torque and that reduces the number of terms in our equations. Be very careful of the angles!

= r F sin
Fwall: cw = (6.0 m)(Fwall)(sin 60°) = (6.0 m)(Fwall)(0.866)
cw = (5.2 m) Fwall

800 N: ccw = (6.0 m)(800 N)(sin 30°) = 2400 m-N
400 N: ccw = (2.0 m)(400 N)(sin 30°) = 400 m-N

Fwall: = 0
Ff: = 0

cw = ccw
(5.2 m) Fwall = 2400 m-N + 400 m-N
(5.2 m) Fwall = 2800 m-N
Fwall = 538 N
Ff = 538 N

µ = 0.45

8.55 A uniform, rectangular, 600 N sign 0.8 m tall and 2.0 m wide is held in a vertical plane, perpendicular to a wall, by a horizontal pin through the top inside corner and by a guy wire that runs from the outer top corner of the sign to a point on the wall 1.5 m above the pin. Calculate the tension on the wire and the force exerted by the pin.


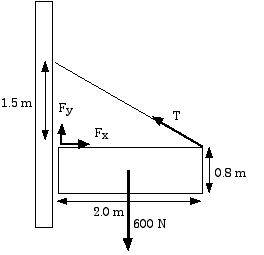
Call the components of the force exerted by the pin Fx and Fy. The angle between the guy wire and the horizontal is

Start with the first condition of equilibrium,

Fx = Fx - T cos 37° = Fx - 0.80 T = 0

Fx = 0.80 T
 Fy = Fy + T sin 37° - 600 N = 0
Fy + 0.60 T = 600 N

This leaves us with two equations but three unknowns, so some additional information is required. Of course, we can get that by applying the second condition of equilibrium. We will calculate torques about the pin. This means the torque caused by the force of the pin is zero. Be careful of the torque for the 600-N weight.

T: ccw = (2.0 m)(T)(sin 37°) =(2.0 m)(T)(0.60) =(1.2 m)T
Fx: = 0
Fy: = 0
W: cw = (1.0 m)(600 N) = 600 m-N
cw = ccw
(1.2 m) T = 600 m-N
T = 500 N
Fx = 0.80 T
Fx = 400 N
Fy = 600 N - 0.60 T
Fy = 600 N - 0.60(500 N)
Fy = 300 N

8.56 A 100 N child sits in the portable high chair shown in the figure. The child sits 20 cm from the top supports and 40 cm from the bottom supports. Determine the forces that hold the chair in place.

 

Hmmmm, . . . My diagram is inconsistent with the statement of the problem. Let's change the parameters to match the diagram. That is, change the problem to read "A 100 N child sits in the portable high chair shown in the figure. The child sits 18 cm from the top supports and 45 cm from the bottom supports. Determine the forces that hold the chair in place."

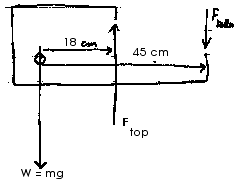
From the first condition of equilibrium, we have

Ftop = Fbottom + 100 N

Calculate torques about the position of the child,

W: = 0
Ftop: ccw = (18 cm)Ftop
Fbottom: cw = (45 cm) Fbottom

Now apply the second condition of equilibrium,

ccw = (18 cm)Ftop = (45 cm) Fvottom = cw
(18 cm)Fttop = (45 cm) Fvottom
Ftop = (45/18) Fbottom
Ftop = 2.5 Fbottom
Ftop = Fbottom + 100 N
2.5 Fbottom = Fbottom + 100 N
1.5 Fbottom = 100 N
Fbottom = 66.7 N

8.74 Figure 8.81, on page 310, shows a person lifting a 30 kg (or 294 newton) mass. When his back is horizontal, as in the sketch, what is the tension T in his back muscles and the compressive force C in his spinal disks?


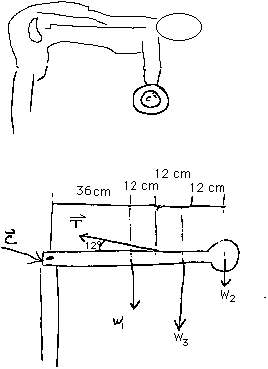
Ooops, I forgot to give you values for w1 and w2; w3 is the weight of 294 N (the 30-kg mass that is being lifted). Read problem 8.73 for those values; w1 = 480 N and ww = 60 N.
From the first condition of equilibrium we have

Cx = T cos 12° = T (cos 12° = 0.9999978 1.00)

and

T sin 12° = 0.208 T = Cy + w1 + w2 + w3
0.208 T = Cy + 480 N + 60 N + 294 N
0.208 T = Cy + 834 N

We now have two equations with three unknowns so we must get additional information from the second condition of equilibrium. We will calculate torques about the hip; that means the torque exerted by the compressive force C will be zero.

C: = 0
T: ccw = (48 cm) T (sin 12°) = (48 cm) T (0.208)
= (9.98 cm) T

w1: cw = (36 cm)(480 N) = 17 280 cm-N
w2: cw = (72 cm)(60 N) = 4 320 cm-N
w3: cw = (48 cm)(294 N) = 14 112 cm-N

ccw = cw
(9.98 cm) T = (17 280 + 4 320 + 14 112) cm-N
(9.98 cm) T = 35 712 cm-N
T = 3 580 N
Cx = 3 580 N
0.208 T = Cy + 834 N
0.208 (3 580 N) = Cy + 834 N
745 N = Cy + 834 N
Cy = - 89 N

The negative sign here simply means that while we assumed that Cy pointed down, Cy actually points up.

| ToC, Ch 8 | Course Calendar|

(c) 2000, Doug Davis; all rights reserved.