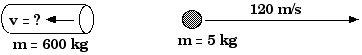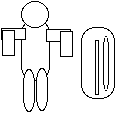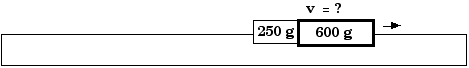Chapter 7; Linear Momentum
and Collisions
7.4, 9, 23. 30, 33, 34, 36,
43, 48, 53, 56, 63

| ToC,
Chapter 7 |
Course
Calendar |

7.4 What is the momentum of a 1200 kg sedan
traveling at 90 km/hr? At what speed must a 3600 kg truck travel to
have the same momentum?
First, change the speed to units of
m/s,
v = 90 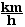
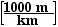
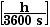 = 25
= 25 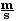
p = m v = [1200 kg] 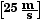 = 30 000
= 30 000 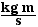
ptruck =
ptruck
vtruck
vtruck
= 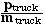 =
= 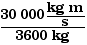 = 8.33
= 8.33 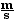
vtruck
= 8.33 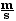
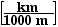
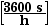 = 30
= 30 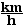
7.9 A 150 gram baseball initially traveling
at 30 m/s is struck by a bat and leaves in the opposite direction at
35 m/s.
a) What is its change in momentum?
b) Is the change in momentum directed along the initial velocity,
the final velocity, or some other direction?
c) What is the impulse delivered by the bat?
d) In hitting a baseball, why is it important to "follow through,"
that is, keep the bat moving and make a full swing, rather than to
stop right after the ball is hit?
Initially, . . . 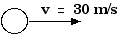
Finally, . . . 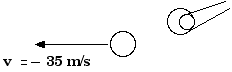
a)  p
=
pf
-
pi
= (0.150 kg)(- 35 m/s) - (0.150 kg)(30 m/s)
p
=
pf
-
pi
= (0.150 kg)(- 35 m/s) - (0.150 kg)(30 m/s)
= (0.150 kg)(- 65 m/s) = - 9.75 kg m/s
b) The change in momentum is opposite to the initial
momentum and/or along the same direction as the final
momentum.
c) "Impulse" is but another word for "change in momentum.
Therefore, the impulse is is - 9.75 kg m/s
d) Impulse =  p
= F
p
= F  t
t
By "following through" there is contact for a longer
time so that a given force can cause a greater change in
momentum. Or a smaller force can cause the same change in
momentum.
7.23 A 600 kg cannon fires a 5 kg
cannonball with a horizontal muzzle velocity of 120 m/s. What is
the recoil velocity of the cannon?
Initially, . . . 
Finally, . . .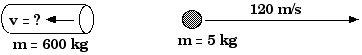
Initially, with cannon and cannon ball both at rest, the total
momentum is zero.
PTot,
initial =
0
By conservation of momentum, we later expect the total momentum to
still be zero. The cannon ball carries momentum to
the right so it is positive. The cannon carries momentum to the
left so it is negative.
PTot, final =
pball
+ pcannon
= (5 kg)(120 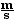 )
+ (600 kg)(vcannon)
= 0
)
+ (600 kg)(vcannon)
= 0
(600 kg)(vcannon)
= - (5 kg)(120 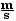 )
)
vcannon
= - 1 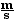
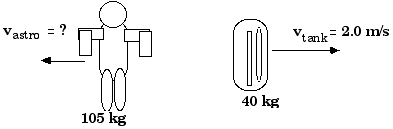
7.30 An astronaut of mass 105 kg
carrying an empty oxygen tank of mass 40 kg is stationary relative
to a nearby space shuttle. She throws the tank away from herself
with a speed of 2 m/s (measured relative to the shuttle). With
what velocity relative to the shuttle does the astronaut start to
move through space?
Initially, with astronaut and oxygen tank both at rest, the
total momentum is zer
PTot, initial
= 0 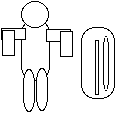
After the astronaut throws the tank, the
total momentum is still zero.
PTot, final
= pastro
+ ptank
= (105 kg)(vastro)
+ (40 kg)( 2.0 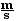 )
= 0
)
= 0
(105 kg)(vastro)
= - (40 kg)( 2.0 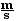 )
)
vastro
= - 0.76 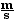
7.33 A 10 000 kg railroad grain car and its load of 3 000 kg
of grain coast along a level track at 3.0 m/s. A door is open
slightly and lets the grain pour out at a rate of 100 kg/s. What
is the speed of the grain car after the grain has all emptied from
the car? What has happened to the initial kinetic energy of the
railroad car?
As the grain falls out of the car, it does not change the
speed of the railroad car and/or the remaining grain in the car.
Much of the initial kinetic energy of the grain and car is "lost".
As the grain falls from the car it carries kinetic energy with it
that is lost to heat as the grain finally comes to rest on the
ground.
7. 34 An inflated rubber raft of mass 30 kg carries two
swimmers of mass 50 kg and 70 kg. The raft and swimmers are
initially floating at rest when the swimmers simultaneously dive
off from the mid-points of opposite ends of the raft, each with a
horizontal velocity of 3 m/s. The 50 kg swimmer dives to the left;
the 70 kg swimmer dives to the right. With what speed and in what
direction does the raft start to move?
Initially, with both divers and the raft at rest, the total
momentum is zero.
PTot,
initial =
0

After the dive, the total momentum is
still zero:
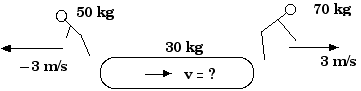
PTot,
final =
pLeftDiver
+ praft
+
pRightDiver
PTot,
final = (50 kg)(- 3 m/s) + (30
kg)(v) + (70 kg)(3 m/s) = 0
- 150 kg m/s + (30 kg)(v) + 210 kg m/s = 0
(30 kg)(v) = - 60 kg m/s
v = - 2 m/s
That is, the raft moves to the left at 2
m/s.
7.36 A 600 g glider sits at rest on an air track when it is
struck by a 250 g glider traveling at 25 cm/s. The two couple and
stick together. What is their velocity?

Initially,
PTot,
initial = (250 g)(25 cm/s) = 6250
gm cm/s.
After the collision,
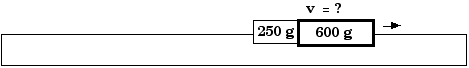
PTot,
final = (850 g) v = 6250 gm cm/s
= PTot,
initial
v = 7.35 cm/s
7.43 A 25 g bullet is fired horizontally with a speed of 100 m/s
into a 5.0 kg block of wood; the wooden block and bullet start to
move off with speed
vf. What is
this speed
vf? The
block is suspended by cords so that it moves in an arc (but does not
rotate) as is illustrated in the figure. What is the height h to
which it rises?
PTot,
final = (5.025 kg)
vf
= (0.025 kg)(100 m/s) =
PTot,
initial
vf
= 0.50 m/s
As the block with embedded bullet starts to
move, it has KE given by
KE = (1/2) M
v2
= (1/2) (5.025
kg) (0.50
m/s)2
= 0.62 J
Relative to the bottom of its swing, its PE is
now zero
So its total energy is E = KE + PE = 0.62 J
At the top of its swing, the block (with embedded bullet) momentarily
comes to rest so its KE there is zero and all of its energy is now PE
= m g h
E = KE + PE = 0 + m g h = m g
h
By energy conservation, this final energy must
still be 0.62 J
E = m g h = (5.025 kg)(9.8
m/s2)
h = 0.62 J
h = 0.0126 m = 1.26 cm
7.48 A stationary 238U nucleus
with atomic mass 238 x 1.67 x
10-27 kg
decays by emitting an alpha particle with atomic mass 4 x 1.67 x
10-27 kg at
a speed of 1.5 x
107 m/s.
What will be the recoil velocity of the resulting
234Th nucleus?
The "pattern" should be clear by now. Initially,
PTot,
initial = 0
After the radioactive decay, the alpha carries
momentum to the right and the thorium nucleus recoils and carries
momentum to the left. The total momentum is still
zero.
PTot,
final = (234 m) (- v) + (4 m)
(1.5 x
107
m/s) = 0 = PTot,
initial
where m = 1.67 x
10-27
kg
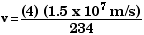
v = 2.56 x
105
m/s
7.53 A 600 g glider moves on an air track with a velocity of 10
cm/s to the right while a 400 g glider moves to the left with a
velocity of 20 cm/s. The two collide elastically. What is the
velocity of each after the collison?
Momentum is always conserved,
PTot,fin
= (600 g)v1f
+ (400 g)v2f
= (600 g)(10 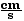 )
+ (400 g)(- 20
)
+ (400 g)(- 20 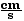 )
)
=
PTot,in
(600)v1f
+ (400)v2f =
- 2000 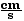
3v1f
+ 2v2f =
- 10 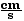
or, if we drop the units, this
becomes
3v1f
+ 2v2f
= - 10
This is one equation with two
unknows, so we must find additional information. Since this is an
elastic collision, we also know that the Kinetic Energy
is conserved.
KETot,fin
= (1/2)(600
g)v1f
2+
(1/2)(400
g)v2f2
=
= (1/2)(600
g)(10
cm/s)2
+ (1/2)(400 g)(- 20
cm/s)2 =
KETot,in
(600)v1f
2+
(400)v2f2
= (600)(10
)2
+ (400)(- 20
)2
3 v1f
2
+ 2
v2f2
= 3 (10
)2
+ 2( - 20
)2
3 v1f 2
+ 2
v2f2
= 1100
Now we have two equations in two
unknowns. We can solve for
v2f
from the earlier one and substitute it
into this equation,
3v1f
+
2v2f
= - 10
2v2f
= -
3v1f
- 10
v2f
= -
1.5v1f
- 5
3 v1f
2
+ 2 [-
1.5v1f
-
5]2
= 1100
3 v1f
2
+ 2
[2.25v1f2
+ 15
v1f
+
25]
= 1100
3 v1f
2
+
4.5v1f2
+ 30
v1f
+ 50 = 1100
7.5v1f2
+ 30
v1f
- 1050 = 0
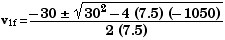
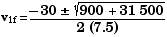
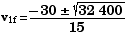
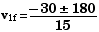
There are two possible solutions, due to the
± in the equation;
Either
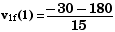 or
or 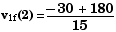
v1f(1)
= - 14 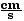 or v1f(2)
= 10
or v1f(2)
= 10 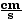
Each of these provides a possible solution for
v2f
v2f(1)
= -
1.5v1f
- 5
v2f(2)
= - 1.5v1f
- 5
v2f(1)
= - 1.5(- 14) - 5
v2f(2)
= - 1.5(10) - 5
v2f(1)
= 21 - 5
v2f2)
= - 15 - 5
v2f(1)
= 16
v2f2)
= - 20
v2f(1)
= 16 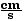 v2f2)
= - 20
v2f2)
= - 20 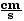
That is, either
v1f(1)
= - 14 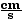 v1f(2)
= 10
v1f(2)
= 10 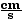
v2f(1)
= 16 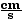 v2f(2)
= - 20
v2f(2)
= - 20 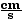
The second set is somewhat interesting for
v1f(2)
= 10 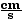 and v2f(2)
= - 20
and v2f(2)
= - 20 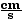 are the initial conditions repeated. This solution is as if the collision
had not occured!
are the initial conditions repeated. This solution is as if the collision
had not occured!
The solution we seek -- the real, physical solution -- is the first
set,
v1f(1)
= - 14 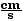 and v2f(1)
= 16
and v2f(1)
= 16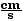
7.56 Below are eight sets of initial conditions for perfectly
elastic collisions on an air track. Glider number two is at rest in
each case. Calculate the velocity of glider number two in each case
and rank them in order of increasing velocity of glider number
one.
glider #2
|
|
mass of
glider #1
|
velocity of
glider #1
|
mass of
glider #2
|
velocity of
glider #2
|
|
A
|
300 g
|
10 cm/s
|
600 g
|
0
|
|
B
|
300 g
|
10 cm/s
|
300 g
|
0
|
|
C
|
300 g
|
10 cm/s
|
200 g
|
0
|
|
D
|
600 g
|
15 cm/s
|
200 g
|
0
|
|
E
|
600 g
|
20 cm/s
|
250 g
|
0
|
|
F
|
300 g
|
25 cm/s
|
350 g
|
0
|
|
G
|
250 g
|
28 cm/s
|
375 g
|
0
|
|
H
|
375 g
|
28 cm/s
|
250 g
|
0
|
Equation 7.13 in the text gives the velocity v2f
for just such a case, 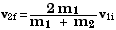 .
Therefore,
.
Therefore,
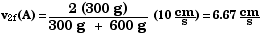
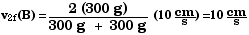
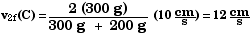
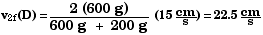
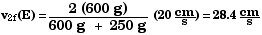
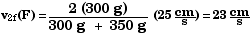
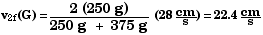
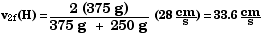
7.63 Exhaust gases leave a certain rocket with a speed of 300
m/s. What must be the mass flow rate in order to lift the 50 000 kg
rocket?
Fthrust
= 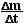 u = M g = Wt
u = M g = Wt
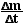 =
= 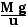
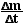 =
= 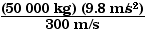
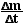 = 1,633
= 1,633 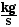

| ToC,
Chapter 7 |
Course
Calendar |

(c) 2002, Doug Davis; all rights reserved

![]()
![]()