PHY 1151

Chapter 6; Work, Power, and Energy
6.5, 14, 19, 22, 36, 38, 45, 55, 61, 72, 75, 88, 92

 

| ToC, Chapter 6 | Course Calendar |

 

6.5 How much work is done by gravity on a skier weighing 600 N who slides 500 m down a hill (measured along the hill) which makes an angle of 30° with the horizontal as sketched in the figure?

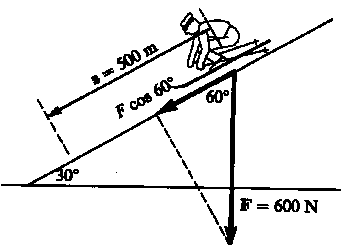
W = F D cos = F D cos 60° = (600 N) (500 m) (0.50) = 150,000 J


6.14 In playing shuffleboard, a long wooden stick is used to give a push to a 0.3 kg puck and cause it to move across the floor. A player pushes with a force of 25 N along the stick, inclined 40° to the ground. The coefficient of friction between puck and floor is 0.10.

a) How much work is done on the puck by the stick as it moves a distance of 0.7 m?
b) What will be the puck's speed after it has moved that 0.7 m, assuming it started at rest?
c) From there the puck leaves the stick and slides across the floor. How far will it slide?

 


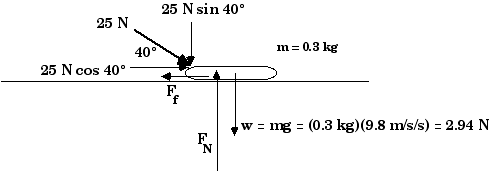
a)
W = F D cos = (25 N) (0.7 m) (0.766) = 13.4 J

Remember, this is the work done by the stick. It is not the total or net work done on the puck (for the friction force also does work on the puck; however the weight and the normal force do not do any work on the puck).

b) Now we need the total work done on the puck.

Wtot = Wnet = Wstick + Wf + WN + Ww

We just found the work done by the stick,

Wstick = 13.4 J

Wf = Ff D cos 180° = Ff (0.7 m) (- 1)

Now we must pause and determine the friction force Ff,

Ff = µ FN = (0.10) FN

And that means we must find the normal force, FN,
The sum of all the y-components of the forces must be zero since there is no acceleration in the y-direction,

Fy = - (25 N)(0.643) + FN - 2.94 N = 0
FN = 2.94 N + 16.07 N = 19.01 N
Ff = µ FN = (0.10) FN = (0.10) (19.01 N) = 1.9 N
Wf = (1.9 N) (0.7 m) ( - 1) = - 1.33 J

The work done by the weight and by the normal force are both zero since these forces are perpendicular to the distance moved,

WN = 0
Ww = 0

Therefore,

Wtot = Wnet = Wstick + Wf + WN + Ww
Wtot = Wnet = 13.4 J - 1.33 J + 0 + 0
Wtot = Wnet = 12.1 J

What does this amount of work cause? From the work-energy theorem (that is, from conservation of energy), we know that work done on an object causes a change in its kinetic energy; that is,

W = KEf - KEi

Since this puck starts at rest, we know

KEi = 0

so that

W = KEf = (1/2) m vf2 = (1/2) (0.3 kg) vf2 = 12.1 J
vf2 = 12.1 J/0.15 kg = 80.7 m2/s2
vf = 9.0 m/s

c) Now what happens? At the end of the 0.7 m the stick no longer exerts a force and work is done only by the friction force. The puck starts out with 12.1 J of KE and finally comes to rest a distance D from where the stick released it. Again, we apply the work-energy theorem,

W = - Ff D = - (1.9 N) D
W = KEf - KEi = 0 - 12.1 J
- ( 1.9 N ) D = - 12.1 J
D = ( 12.1 / 1.9 ) m
D = 6.4 m

6.19 An electric bill lists 1284 kW-h as the energy used for a month. If the charge is 11.5 cents per kW-h, what is the total bill? How many joules of energy were used that month?

Cost = (1284 kW-h)($0.115/kW-h) = $147.66

E = 1284 kW-h = 1284 x 103 W-h [ (J/s)/W] ( 3600 s/h )
E = 4.62 x 106 J

6.22 The output of a common student laboratory laser is about 250 milliwatts. How much energy is delivered in one hour?

E = P t = (0.25 mW) (1 h) () () () = 0.9 J

6.36 The power of a boat’s motor at a speed of 40.0 km/h is 22.0 kW. If the power is 15% greater while pulling a skier at the same speed, what is the tension in the tow rope?

P = F v (assuming F and v are parallel)

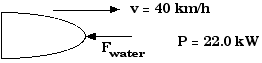
P = F v

As usual, we must change the speed from units of km/h to units of m/s

v = 40 () () = 11.11
F = =
F = 1980 N

This is Fwater, the force the water exerts on the boat.
When a skier is towed the power is 15% greater,

P' = (1.15)(22 kW) = 25.3 kW

 


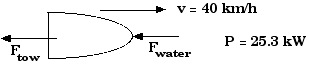
Now the net force is

Fnet = Ftow + Fwater

and that is the force that goes into

P = F v
F = = = 2277 N
Ftow = Fnet - Fwater = 2277 N - 1980 N
Ftow = 297 N

This is the tension in the ski tow rope

6.38 What is the kinetic energy of a 1750 kg car traveling at 80 km/h?

KE = (1/2) m v2

As usual, we must change the speed from units of km/h to units of m/s

v = 80 (km/h) (h/3600 s) (1000 m/km) = 22.22 m/s
KE = (1/2) m v2
KE = (1/2) (1750 kg) (22.22 m/s)2 = 4.32 x 105 J

6.45 Below are data for eight air track gliders with different masses and speeds. Calculate the values of their kinetic energies.
mass (kg)
speed (m/s)
A
0.225 kg
0.85 m/s
B
0.225
0.90
C
0.250
0.35
D
0.250
0.50
E
0.267
0.65
F
0.315
0.82
G
0.450
0.45
H
0.450
0.52
KE = (1/2) m v2
A) KE = (1/2) (0.225) (0.85 m/s)2 = 0.0813 J
B) KE = (1/2) (0.225) (0.90 m/s)2 = 0.0911 J
C) KE = (1/2) (0.250) (0.35 m/s)2 = 0.0153 J
D) KE = (1/2) (0.250) (0.50 m/s)2 = 0.0313 J
E) KE = (1/2) (0.267) (0.65 m/s)2 = 0.0564 J
F) KE = (1/2) (0.315) (0.82 m/s)2 = 0.1059 J
G) KE = (1/2) (0.450) (0.45 m/s)2 = 0.0456 J
H) KE = (1/2) (0.450) (0.52 m/s)2 = 0.0608 J

6.55 A ski slope drops at an angle of 20° and is 600 m long. Find the change in potential energy of a 70-kg skier who goes down this slope.


PE = m g h = (70 kg)(9.8 m/s2)(205 m) = 141,000 J = 141 kJ

6.61 In loading a certain dart gun, the dart is pushed in 12 cm before the gun is cocked. A force of 20 N is required at the end. Find the spring constant of the spring in the gun. Find the total amount of energy stored in the spring.

F = k x
k = = = 167
PEel = (1/2) k x2
PEel = (1/2) (167 N/m)(0.12 m)2
PEel = 1.2 J

6.72 An arrow of mass 0.1 kg is fired directly upward by an archer who exerts an average force of 75 N on a bowstring that is pulled back 0.6 m. After it comes down, the arrow penetrates 20 cm vertically into the ground. Use the ideas of work and energy to answer the following:

a) With what speed does the arrow leave the bow?
b) How high does the arrow go?
c) What average upward force does the ground exert on the arrow while stopping it?
a)
Ef = (1/2) m v2 = Ei = W = (75 N)(0.6 m) =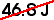

Yikes! My apologies for that arithmetic error.

75 x 0.6 = 45

Ef = (1/2) m v2 = Ei = W = (75 N)(0.6 m) =45.00

(1/2) (0.1 kg) v2 = 45.0 J
v2 = 900 m2/s2
v = 30 m/s

 

b)
Ef = m g h = 45 J
(0.1 kg) (9.8 m/s2) h = 45 J
h = 45.9 m

c)

W = F D = 45.0 J
F (0.2 m) = 45.0 J
F = 225 N

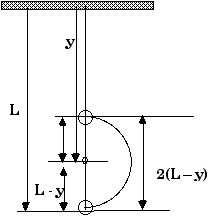
6.75 A ball is attached to a cord of length L which is initially held horizontal from a fixed support at P as sketched in the figure. The ball is released from rest at point A.

a) Find its speed at point B, the bottom of the swing.
A peg is fixed at point O, a distance y directly below point P. The cord hits the peg and the ball swings upward in an arc as shown.
b) Find the ball's speed at point C when the cord between it and the peg is horizontal.
c) Find the ball's height (relative to its starting position) at point D, the top of its swing after hitting the peg (Assume y > L/2).
d) Find the ball's speed at point D, the top of its swing after hitting the peg.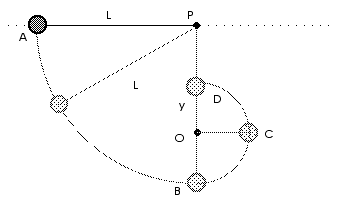

a) At position A, vA = 0 or KEA = 0
If we measure all the vertical distances from yB = 0 at position B, then at A, the mass has a height yA = L, so that

PEA = m g yA = m g L

( This choice for yB = 0 means PEB = 0 ).

Therefore, the total energy at A, EA, is

EA = KEA + PEA = 0 + m g L = m g L

Energy is conserved so

EB = EA
KEB = (1/2) m vB2
PEB = m g yB = 0

Remember, we have measured vertical distances here so we have set yB = 0. That means our total energy at position B is

EB = KEB + PEB = (1/2) m vB2 + 0 = (1/2) m vB2
EB = (1/2) m vB2 = m g L = EA
vB2 = 2 g L
vB =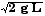

A peg is fixed at point O, a distance y directly below point P. The cord hits the peg and the ball swings upward in an arc as shown.
c) At position C, the (vertical) height above position B is

yC = (L - y)

Energy is conserved so

EC = EA
KEC = m vC2
PEC = m g yC = m g (L - y)

That means our total energy at position C is

EC = KEC + PEC = (1/2) m vC2 + m g (L - y)
EB = (1/2) m vC2 + m g (L - y) = m g L = EA
(1/2) m vC2 + m g L - m g y = m g L
(1/2) m vC2 = m g y
vC2 = 2 g y
vC =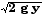

d) At position D, the (vertical) height above position B is

yD = 2 (L - y)

as can be seen by taking a more careful look at the diagram.

 


Energy is conserved so
ED = EA
KED = (1/2) m vD2
PED = m g yD = m g [2 (L - y)]

That means our total energy at position D is

ED = KEC + PEC = (1/2) m vC2 + m g [2 (L - y)]
ED = (1/2) m vD2 + m g [ 2 (L - y) ] = m g L = EA
(1/2) m vD2 + 2 m g L - 2 m g y = m g L
(1/2) m vD2 = 2 m g y - m g L
vD2 = 2 g ( 2 y - L )
vD =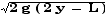

6.88 Calculate escape velocity from the surface of Mars.

From Equation 6.23, we know the escape speed in general,
vesc =
vesc =

where we have used values of M and R from Table 5.1 on page 162 of the text and been careful to put numbers in with consistent units. Thus,

vesc = 5010
vesc = 5010 ()() = 18,000
vesc = 11,000

Remember, escape velocity from Earth's surface is about 25,000 mi/hr, about twice escape velocity from Mars.

6.92 The pilot of the first successful human-powered, heavier-than-air flight could generate an average of 0.32 kW (0.43 hp) during the flight. The aircraft covered 2.4 km at an average speed of 4.1 m/s. How much energy was expended during the flight?

Energy = power x time

v =
t = = = = 585 s
Energy = (0.32 kW)(585 s)
Energy = (320 W)(585 s)( )
Energy = 187,000 J

 

| ToC, Chapter 6 | Course Calendar |

 

(c) 2002, Doug Davis; all rights reserved.