
PHY 1151
Doug Davis

PHY 1151
Doug Davis
![]()
| ToC, Chapter 3 | Course Calendar |
![]()
All four of the resultants R are identical. The order in which we add vectors does not
make any difference.
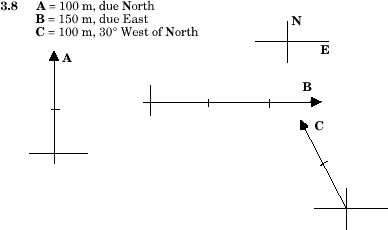
3.15 A = 10 km, 60° W of NB = 25 km, 37° E of S
C = 10 km, 53° W of S
As always, sketches are important. Draw these vectors first; only then should you
begin your calculations.
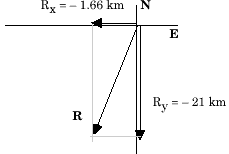
3.23 Now we want to add the components that we calculated in Problem 3.15.
B x = 15 km
Cx = - 8 km
Rx = - 1.66 km
By = - 20 km
Cy = - 6 km
Ry = - 21 km
Now, what is the direction of the resultant R?
![]()
That is, R =21.1 km, 4.5° West of South.
3.35 A stone is thrown at an angle of 30° above the horizontal from the top of a cliff15 meters above a wide river with an initial velocity of vi = 5 m/s.
a) What are the horizontal and vertical components of its initial velocity?b) How long does it take to hit the water below?
c) How far from the side of the cliff does it hit the water?
d) What is its velocity when it hits the water?
e) What is its speed when it hits the water?
3.41 A book is thrown horizontally out a residence hall window 7.00 m above the grass outside the residence hall. The book lands on the grass 8.00 m from the base of the hall. Find the velocity with which the book was thrown.Since the book initially moves horizontally, we immediately know vy,i = 0 and the vertical motion is simply free fall from rest. The time it takes the book to "fall" the 7.00 m to the ground can be found from
y = yi + vy,i t + ( 1/2 ) a t2 We may as well take the ground to be y = 0 and that makes the initial vertical
position of the book yi = + 7.00 m.
y = yi + vy,i t + ( 1/2 ) a t2 0 = 7.00 m + 0 + ( 1/2 ) (&endash; 9.8 m/s2 ) t2
4.9 t2 = 7 s2
t2 = 1.43 s2
t = 1.2 s
In that time of 1.2 s, the book travels horizontally a distance of 8 m so its horizontal velocity must be
vx = ( 8 m ) / ( 1.2 s ) = 6.67 m/s The horizontal component of the velocity remains constant so
vx,i = vx = 6.67 m/s
3.43 Cliff divers at Acapulco jump into the sea from a cliff 36 meters high. At the level of the sea, there is an outcropping of rock that sticks out a horizontal distance of 6 meters. With what minimum horizontal velocity must the cliff divers leave the top of the cliff if they are to miss this rocky outcropping?Assume the divers have an initial velocity that is horizontal&emdash;this means the initial vertical component of velocity is zero, vy,i = 0. Then the time for the dive is given by
y = yi + vy,i t + ( 1/2 ) ay t2 0 = 36 m + 0 + ( 1/2 ) ay t2
0 = 36 m + 0 + ( 1/2 ) ( - 9.8 m/s2 ) t2
where we have taken the coordinate system to be such that y = 0 at the sea and yi = 36 m at the cliff where the divers begin. Now we can solve for the time,
(4.9 m/s2 ) t2 = 36 m t2 = 7.35 s2
t = 2.7 s
During that time of 2.7 s that the diver is in the air, he must move horizontally a distance x = 6 m to avoid the rocks below. Since his horizontal velocity remains constant, that means
vx,i = vx = 6 m 2.7 s = 2.2 m/s
vx,i = 2.2 m/s
3.54 A mountain climber is stranded on a ledge 300 m above the ground. Rescuers on the ground want to shoot a projectile to him with a rope attached to it. If the projectile is directed upward at an initial angle of 35° and fired at the ledge from a horizontal distance of 500 m, determine the initial speed the projectile must have in order to land on the ledge. (Simply redrawing the diagram so the motion is from left to right may make it a little easier).How long does it take the projectile to reach the cliff -- that is, to have the horizontal position of the cliff?
x = xi + vx,i t + ( 1/2 ) ax t2 x = 0 + (0.82 v )t + 0 = 500 m
t = (500 m)/(0.82 v)
In that amount of time, the vertical displacement of the projectile must equal the vertical displacement of the ledge, 300 m,
y = yi + vy,i t + ( 1/2 ) ay t2 300 m = 0 + (0.57 v) [(500 m)/(0.82 v)] + ( 1/2 ) ( - 9.8 m/s2 ) [(500 m)/(0.82 v)]2
300 m = 0 + 348 m - 1,822,000 (m3/s2)(1/v2)
- 48 m = - 1,822,000 (m3/s2)(1/v2)
48 m = 1,822,000 (m3/s2)(1/v2)
v2 = (1,822,000 / 48 ) (m2/s2)
v2 = 37958 (m2/s2)
v = 195 m/s
3.67 A projectile is fired with initial velocity of 15 m/s at 53° above the horizontal from the foot of a plane inclined 20° above the horizontal as sketched in the figure below. How far up the inclined plane does the projectile strike the plane?We need to find equations for the projectile's path and for the inclined plane and see where those two intersect (that is, where they have the same value). The projectile moves along a path given by
x = xi + vx,i t + ( 1/2 ) ax t2 and
y = yi + vy,i t + ( 1/2 ) ay t2 where vx,i = (15 m/s) cos 53° = (15 m/s) (0.6) = 9 m/s
and vy,i = (15 m/s) sin 53° = (15 m/s) (0.8) = 12 m/s
and ax = 0
and ay = - 9.8 m/s2
Of course, xi = 0 and yi = 0.
That is,
x = 0 + (9 m/s) t + 0 and
y = 0 + (12 m/s) t + ( 1/2 ) ( - 9.8 m/s2) t2 From the x-equation, we may solve for t,
t = (x)/(9 m/s) and then substitute that into the y-equation,
y = 0 + (12 m/s) t + ( 1/2 ) ( - 9.8 m/s2) t2 y = 0 + (12 m/s) [(x)/(9 m/s)] + ( 1/2 ) ( - 9.8 m/s2) [(x)/(9 m/s)]2
y = 1.33 x - (0.605m) x2
If we are careful to measure both x and y only in meters, then we may drop the units and it may be easier to solve this problem if this equation is written as
y = 1.33 x - 0.605 x2 Notice that this is a quadratic equation -- the equation of a parabola curved downward. That is what we would expect. Now, what is the equation of the inclined plane?
tan 20° = opposite / adjacent = y / x y = x tan 20° = 0.36 x
y = 0.36 x
Now we have two equations for y; set those equal to each other,
y = 0.36 x = 1.33 x ; 0.605 x2 0.605 x2 = 0.97 x
0.605 x = 0.97
x = 0.97 / 0.605 m = 1.60 m
y = 0.36 x = (0.36) (1.60 m) = 0.58 m
| ToC, Chapter 3 | Course Calendar |
![]()
(c) 2002, Doug Davis; all rights reserved