PHY 1151

Doug Davis

Ch 2, Motion in 1D:

Everything will come from our "Big Three Kinetmatics Equations":

2.10 A bicyclist travels with an average velocity of 15 km/h, North for 20 minutes. What is his displacement?

The definition of average velocity, v = can be solved for Ds = v Dt

Ds = v Dt = (15 ) (20 min) ( ) = 5 km

 

2.12 The speed of sound in air is about 330 m/s. You observe a lightning bolt strike a tree 1.5 km away. How much time will elapse between your seeing the lightning bolt and hearing the thunder that accompanies it? Why do you not need to take into account the speed of light?

The definition of average velocity, v = can be solved for Dt =

Dt = = = = 4.5 s

2.16 A car accelerates from rest to 90 km/h in 8.8 s. What is its average acceleration in m/s²?

Use the basic definition of acceleration, a =

It may be easier, or more convenient, to change the velocity of 90 km/hr into units of m/s early on,

v_f = 90 ( ) ( ) ( ) = 25

a = = = 2.8 m/s²

2.19 A jet aircraft landing on an aircraft carrier is brought to a complete stop (v_f = 0) from a (an initial) velocity of (v_i= ) 215 km/h in 2.7 seconds. What is its average acceleration in m/s²?

Again, use the basic definition of acceleration, a =

As before, it may be easier, or more convenient, to change the velocity of 90 km/hr into units of m/s early on,

v_i= 215 ( ) ( ) ( ) = 59.8

v_f = 0

a = = = = - 22.1 m/s²

2.23 A certain car has an acceleration of 2.4 m/s². Assume that its acceleration remains constant. Starting from rest, how long does the car require to reach a velocity of 90 km/h? How far does it travel while reaching that velocity?

It may be easier, or more convenient, to change the velocity of 90 km/hr into units of m/s early on,

v_f = 90 ( ) ( ) ( ) = 25

We can solve the equation v = v_i + a t for the time t, t = .

"Starting from rest" means v_i = 0 so that becomes t =

t = = = 10.4 s

Now that we know "how long" we can use the displacement-time equation, with this time, to determine "how far".

s = s_i + v_i t + a t²

s = 0 + 0 (10.4 s) + (2.4 m/s2) (10.4 s)²

s = 128 m

2.38 In passing a slow truck you must accelerate from 50 km/h to 90 km/h. What must your acceleration be so you can complete your passing maneuver in 1.0 km?

We know the velocities and the displacement involved and don't really care about the time so we can use the equation

It may be easier, or more convenient, to change the velocities of 50 km/hr and 90 km/hr into units of m/s early on,

v_f = 50 ( ) ( ) ( ) = 13.9

v_f = 90 ( ) ( ) ( ) = 25

 

v² = v_i² + 2 a (s - s_i)

( 25 )² = ( 13.9 )² + 2 a ( 1000 m )

625 m²/s² = 193 m²/s² + (2000 m) a

(2000 m) a = (625 - 193) m²/s² = 432 m²/s²

a = = 0.216 m/s²

2.46 A car, speeding at 130 km/h passes a police car at rest. Just as the speeding motorist passes the police car, the police car begins pursuit. If the police car maintains a constant acceleration of 5.8 m/s², when and where will the speeding motorist be overtaken?

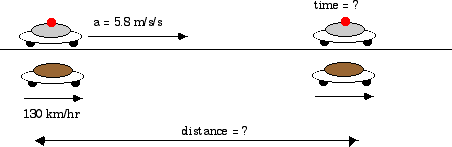
We can make life a little easier by changing the motorist's velocity of 130 km/hr into units of m/s.

v_mot = 130 ( ) ( ) ( ) = 36.1

The motorist travels at constant velocity of 130 km/hr or 36.1 m/s so the motorist's acceleration is zero, a_mot = 0 .

The motorist's position or displacement is given by

s_mot = s_{mot, i} + v_{mot, i} t + a_mot t²

s_mot = 0 + (36.1 m/s) t + (0) t²

s_mot = (36.1 m/s) t

The police car starts from rest so v_{pol, i} = 0 but then accelerates at 5.8 m/s².

The police car's displacement or position is given by

s_pol = s_{pol, i} + v_{pol, i} t + a_pol t²

s_pol = 0 + (0) t + (5.8 m/s²) t²

s_pol = (5.8 m/s²) t²

For what time and where are these two displacements equal?

The motorist's position or displacement is given by

The police car's displacement or position is given by

s_pol = (5.8 m/s²) t²

For what time and where are these two displacements equal? Set the two equations equal to each other.

s_pol = (5.8 m/s²) t² = (36.1 m/s) t = s_mot

(5.8 m/s²) t² = (36.1 m/s) t

(5.8 m/s²) t = (36.1 m/s)

t = s = 12.5

t = 12.5 s

That tells us when. We can put that back into either displacement equation to determine where. The motorist's displacement, since it has only a term with time and not with time-squared, is the easier to use.

And we can check this answer by evaluating the police car's displacement.

s_pol = (5.8 m/s²) t² = (5.8 m/s²) (12.5 s)² = 453 m

The answers agree to two significant figures. The time of 12.5 s was really 12.448 s and we would expect a closer agreement between the two answers if we kept more significant figures in our answer for the time. But more significant figures are not warranted because the police car's acceleration of 5.8 m/s² is given only to two significant figures.

2.48 A late commuter, sprinting at 8 m/s, is 30 m away from the rear door of a commuter train when it starts to pull out of the station with an acceleration of 1 m/s². Can the commuter catch the train (if the platform is long enough)?

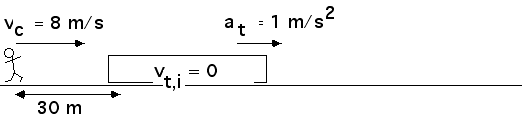
This time, notice that the commuter and the train start from different places. That is, they have different initial displacements. We can take care of that with

The initial velocities of commuter and train are

Their two accelerations are

We can write equations for the displacement of the commuter and for the displacement of the train

s_c = s_c,i + v_c,i t + a_c t²; and s_t = s_t,i + v_t,i t + a_t t²

s_c = 0 + (8 m/s) t + (0) t²; and s_t = 30 m + (0) t + (1 m/s²) t²

s_c = (8 m/s) t; and s_t = 30 m + (1 m/s²) t²

Now set these two equations equal to each other and solve for the time t. If there is no solution, then the commuter can not catch the train. If there is a solution, that value of time t tells us when the commuter catches the train. We can then use that value of time t to evaluate the displacement from either equation.

s_t = 30 m + (1 m/s²) t² = (8 m/s) t = s_c

30 m + (1 m/s²) t² - (8 m/s) t = 0

(1 m/s²) t² - (8 m/s) t + 30 m = 0

(1 m/s²) t² - (16 m/s) t + 60 m = 0

If time t is measured in seconds, then each term in this equation has units of m (for meters) and we may eliminate the units and simply write

This is now a quadratic equation of the form

and has a solution in the form of

x =

For our present equation, we have a = 1, b = - 16, and c = 60.

Therefore,

t =

t =

t =

t =

t =

There are two solutions:

t₁ = s = 10 s

and

t₂ = s = 6 s

What do these two solutions mean?

At t = 6 seconds, the commuter catches up with the train. This is the "real solution". At t = 6 seconds, the commuter catches the train and the race is over. However, the mathematics does not stop there. If the commuter continues to run, he will pass the train and the train will catch up with him at t = 10 seconds!

2.51 While standing still, a police car is passed by a speeding car traveling at a constant 120 km/h. The policeman waits 2 seconds before deciding to pursue. What must be his acceleration in order to catch the speeding car within three kilometers?

 

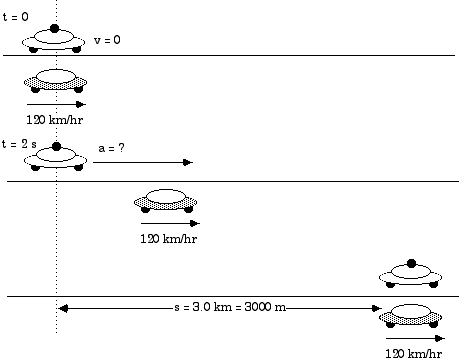
First, let's do the easy conversion of the car's speed of 120 km/hr to m/s

vcar = 120 = 33.3

Remember, since the car travels at constant velocity, this is its initial velocity and we know its acceleration is zero, a_car = 0

The police car's initial velocity is zero, v_{pol, i} = 0 and we are trying to solve for its acceleration, a_pol = ?

We can immediately write the equation for the displacement or position of the car,

s_car = s_car,i + v_car,i t + a_car t²

s_car = 0 + (33.3 ) t + (0) t²

s_car = (33.3 ) t

We can set this equal to 3 km or 3,000 m and find out how long the car travels before the police car catches up with it.

s_car = (33.3 ) t = 3,000 m

t = = 90 s

(3 km is a l-o-n-g distance for catching the speeding motorist).

Remember, the policeman waits for 2 s before beginning pursuit. Therefore, the time required for the police car to travel 3,000 m is 88 s. We can write an equation for the displacement of the police car and find the acceleration necessary.

s_pol = s_pol,i + v_pol,i t + a_pol t²

3,000 m = 0 + (0) (88 s) + apol (88 s)²

3,000 m = a_pol (88 s)²

3,000 m = (3872 s²) a_pol

a_pol =

a_pol = 0.77 m/s²

2.62 How fast must a stone be thrown, straight up, to just reach the top of a building that is 10 m high?

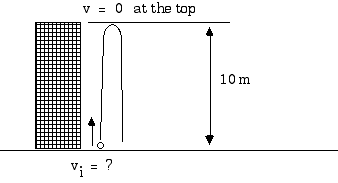
Throughout the stone's flight, its acceleration is a = - 9.8 m/s² (for convenience, we will use the approximation that its acceleration is a = - 10 m/s²). This means we have taken up as positive.

Since we do not care about the time, we can use the third of our "big three" equations,

or

or

We will measure everything from the ground so s_i = 0. At the top, where s = 10 m, the stone stops momentarily so v = 0.

2.66 Cliff divers in Acapulco dive from rocks about 35 m above the water. Neglecting air resistance, what is their velocity as they hit the water?

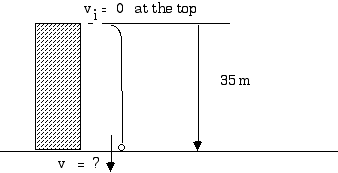
Everything is happening in the "down" direction, so we may as well take down as positive for this case. If down is positive, then the acceleration is a = + 10 m/s² (the acceleration is really + 9.8 m/s2, but we will make the arithmetic easier by using this approximation). We will measure distances from the top of the cliff.

There, at the top of the cliff,

Since we are not interested in the time, we can use the third of our "big three" equations,

2.86 In the mid-1960’s McGill University, in Montreal, launched high-altitude weather sensors by firing them from a cannon made from two World War II Navy cannon bolted together for a total length of 18 m. It was proposed that they use this arrangement to launch a satellite. Orbital speed of a satellite is about 29 000 km/h. What would have been the average acceleration throughout the 18 m length of the cannon to have a muzzle velocity of 29 000 km/h?

While it is easier to think of orbital velocity in terms of km/h, it is easier to do the calculations with this velocity in units of m/s.

v = 29 000 = 8060

v² = v_i² + 2 a ( s - s_i)

(8060 )² = 0² + 2 a ( 18 m - 0)

(8060 )² = 02 + 2 a ( 18 m - 0)

64 963 600 = (36 m) a

a =

a = 1 804 544 m/s²

a = 1 800 00 m/s²

We will later see that there is an important connection between forces and accelerations. To experience such an enormous acceleration, the payload would have to be able to withstand enormous forces!

2.92 A falling flower pot takes 0.25 s to pass by a window 1.5 m high. How far above the top of the window was the balcony from which the flower pot fell?

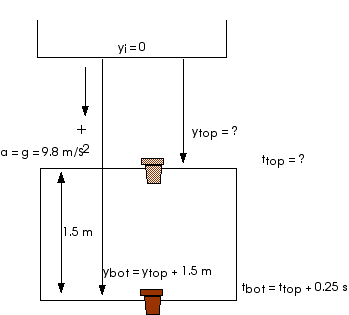
(Only) After the diagram is carefully drawn and labeled, we can start writing equations (notice that I have taken down as positive):

We are looking for the distance I have labeled y_top, the distance from the balcony above to the top of the window.

Since we are measuring distances from the balcony above, we know y_i = 0. Since the flower pot falls from rest, we know v_yi = 0. Then our equations for y_top and y_bot can be simplified to become just

But we also know y_bot = y_top + 1.5 m and t_bot = t_top + 0.25 s.

Subtract one equation from the other,

This is really t_top but I dropped the subscript to make things look "prettier" (ie, less messy or less busy).

But we want the distance to the top,

2.96 Poor Wyl E Coyote is at it again. Attempting to catch the Road Runner he falls from the top of a 400 m cliff. He is wearing an Acme Fireworks rocket but requires 6 seconds to light the fuse and ignite the rocket. The burning rocket gives him an upward acceleration so that his velocity just reaches zero as he reaches the bottom.

a) How far has he fallen before the rocket starts?

b) What is his upward acceleration in order to have this gentle landing?

But, alas, as Edsel Murphy would have it, the Acme rocket does not shut off. Nor is the Coyote able to release himself from the rocket. Therefore, the rocket now carries him upward with this same acceleration for an additional 5 seconds before it depletes its fuel.

c) How high is he then (as the fuel runs out)?

d) How fast is he moving then?

e) How high -- how far above the canyon floor -- does the Coyote eventually go?

f) How fast is he going as he hits the canyon floor this time?

a)

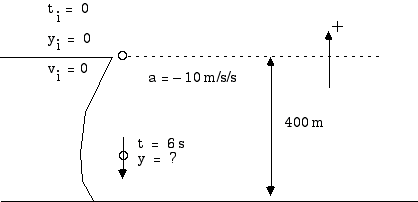
In t = 6 s, the Coyote has fallen a distance s (or y) given by

s = s_i + v_i t + a t²

or

y = y_i+ v_y,i t + a_y t²

We will measure displacements from the cliff so that s_i = y_i = 0

y = (0) + (0) t + (- 10 m/s²) t²

At time t = 6 s, this becomes

y = (0) + (0) (6 s) + (- 10 m/s²) (6 s)²

y = (- 10 m/s²) (36 s²)

y = - 180 m

a) y = - 180 m, that is, 180 m below the top of the cliff (or 220 above the canyon floor, if you prefer).

The burning rocket gives him an upward acceleration so that his velocity just reaches zero as he reaches the bottom.

b) What is his upward acceleration in order to have this gentle landing?

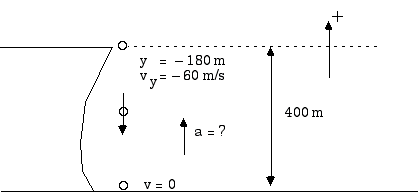
Be careful. It might be better to write this equation with subscripts 1 and 2.

Now v₁ and s₁ refer to the situation we found at the end of part a),

And v₂ and s₂ refer to the velocity and position right at the canyon floor,

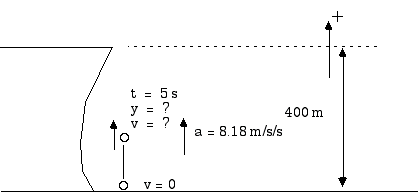
From the floor of the canyon, from being at rest, Wyl E Coyote accelerates upward with an acceleration of 8.18 m/s². We could start everything over at this point and measure distances from the floor of the canyon. However, it is just as good -- and just as easy -- to leave the origin where it was and continue to measure distances from the top of the cliff. With that reference frame, the initial position for this part of the trip is

That is, 297 m below the cliff (or 103 m above the canyon floor).

d) How fast is he moving then?

Note that the positive value for the velocity means the Coyote is moving up when the fuel runs out.

e)

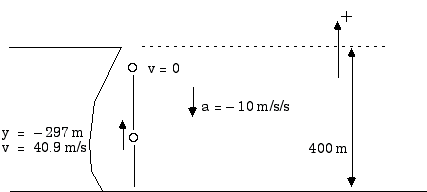
Now the Coyote is in "free fall" with a = - g = - 10 m/s² (yes, his acceleration is really a = - g = - 9.8 m/s² but we will again use this approximation just to keep the arithmetic somewhat easier and to be consistent with the earlier use of it).

The equation connecting velocity, acceleration, and distance is

or

where s₁ = y₁ = - 297 m, v_y1 = v₁ = 40.9 m/s, and v_y2 = v₂ = 0 and we are wanting to find s₂ or y₂.

Remember, that is 213 m below the cliff or 187 m above the canyon floor.

f) Alas, the rocket fuel is finally depleted and our Coyote falls this 187 m to the canyon floor below. What is his impact velocity?

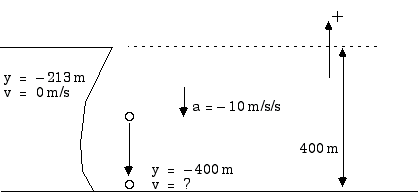
Again, since we are not particularly interested in the time we can use

or

Either + 61.2 m/s or - 61.2 m/s is a solution to the mathematics. What is happening physically? The Coyote is falling down so we must choose the negative solution,

2.101 The figure below is a position-time graph for a lab cart traveling along a straight track in a Physics lab. Determine the time(s) that the cart

a) has its greatest velocity.

b) has constant velocity.

c) is moving backward.

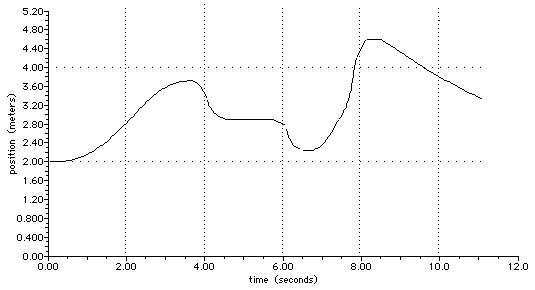
a) has its greatest velocity. Velocity is the slope of the line and that seems to be greatest around 7.5 seconds or so.

b) has constant velocity. This means constant slope. From about 4.5 s to 5.5 s the slope and velocity are constant at zero. From about 1.5 s to about 3.0 s the slope and velocity seem to be constant with a value of about 0.4 m/s. From about 8.5 s on the slope and velocity seem to be constant with a value of about - 0.6 m/s

c) is moving backward. "Moving backward" means a negative slope. That occurs between 3.5 s and 4.5 s, between 5.75 s and 6.5 s, and from 8.25 s on to the end of the graph around 11 s.

2.102 The Figure below is a position-time graph. From it construct the corresponding velocity-time and acceleration-time graph. (That is, do not worry about the acceleration-time graph as the data given is really not sufficient).

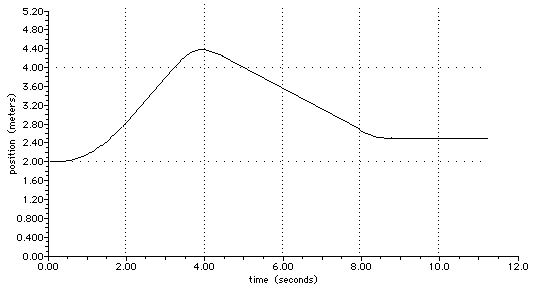
The velocity is the slope of the line on a position-time graph. From about 1.75 s to about 3.5 s the position increases at a rate of 1.0 m/s; that is, the velocity is 1.0 m/s during that time. Then the velocity starts to decrease, passing through zero at about 4.0 s. By about 4.25 s, the position is decreasing at a steady rate of 0.5 m/s so the velocity is a constant - 0.5 m/s up until about t = 8.0 s. Then the velocity approaches zero and remains at zero from about 8.25 seconds on.

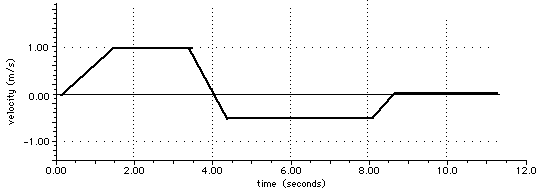
There is really insufficient information to accurately find the acceleration.

2.106 -- Oops! I seem to have 2.106 on here twice. Take your pick. I hope the two solutions are consistent.--

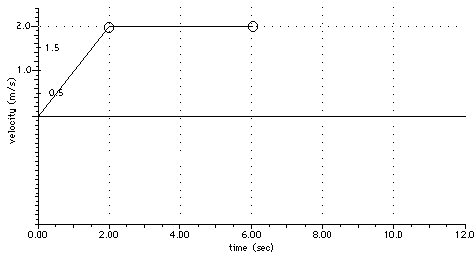
2.106 The Figure below is an acceleration-time graph. Use it to construct corresponding position-time and velocity-time graphs. Start the car from rest, vi = 0, at x = 0 for t = 0.

During the time from 0 s to 2.0 s, the acceleration is a = + 1 m/s2.

v = v_i + a t

v(2 s) = 0 + (1 m/s²) ( 2 s) = 2 m/s

From t = 2 s to t = 6 s, the acceleration is zero

so the velocity remains constant at v = 2 m/s.

During the time from 6.0 s to 8.0 s, the acceleration is a = - 1 m/s².

From t = 8 s to t = 12 s, the acceleration is zero

so the velocity remains constant at v = 0.

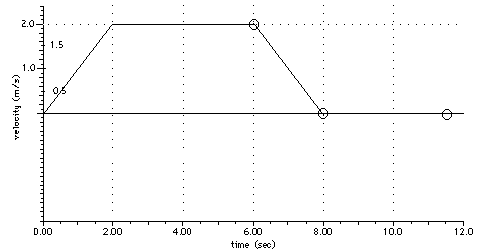
Now, for the position or displacement.

During the time from 0 s to 2.0 s, the acceleration is a = + 1 m/s².

s = s_i + v_i t + a t²

s (2 s) = 0 + 0 (2 s) + ( 1 m/s²) (2 s)²

s (2 s) = 2 m

It is only a coincidence that the numerical value of the displacement happens to be equal to the numerical value of the velocity for time t = 2 s.

From t = 0 to t = 2, the position-time curve is a parabola that goes through (0, 0) and (2, 2). From t = 2s to t = 6 s, the velocity remains constant at v = 2.0 m/s so the position-time curve is a straight line with a slope of 2.0 m/s. This means the displacement for t = 6 s is

Dt = 4 s since this piece of the problem starts at t_i = 2 s.

From t = 6 s to t = 8 s, the acceleration is - 1.0 m/s2, with the velocity going from 2.0 m/s to zero during that time. At t = 6 s, which we will call ti = 0, the displacement is 10 m. We can calculate the displacement at the end of this Dt = 2 s interval by

s = s_i + v_i t + a t²

s = 10 m + (2 m/s) (2 s) + (- 1 m/s²) (2 s)²

s = ( 10 + 4 - 2 ) m = 12 m

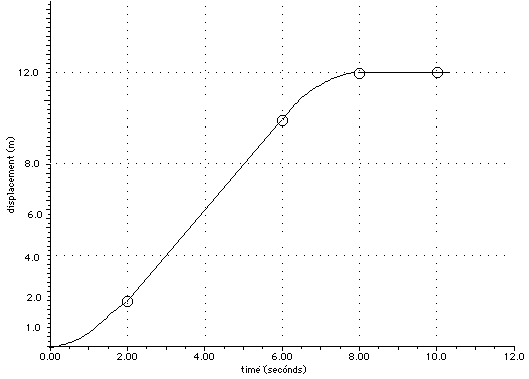
We can put all these together on a graph. The circles on the graph above indicate the displacements we have actually calculated. The curve from 0 to 2 s is a parabola. The line from 2 s to 6 s is a straight line. The curve from 6 s to 8 s is a parabola. And the line from 8 s on is a straight, horizontal line, corresponding to zero velocity.

2.106 (second version!) The figure below is an acceleration-time graph. Use it to construct the corresponding position-time and velocity-time graphs. Start the car (or whatever) from rest, vi = 0, at x = 0 for t = 0.

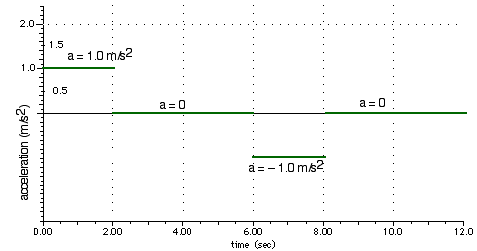
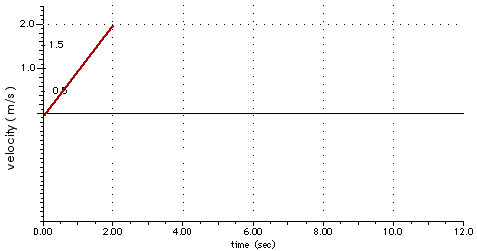
First, look at the motion for time between 0 and 2.0 s (0 < t < 2.0 s) for which the acceleration is a = 1.0 m/s². We can calculate the velocity from

At the end of that 2.0 seconds (at t = 2.0 s), the velocity is 2 m/s. That appears on a velocity-time graph as

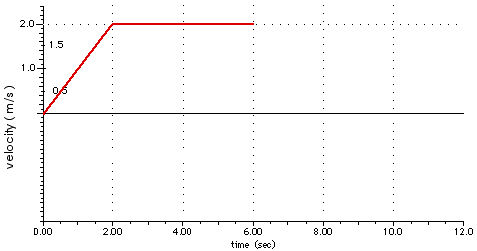
From2.0 to 6.0 seconds-that is, for 2.0 s < t < 6.0 s - the acceleration is zero ( a = 0 ) which just means the velocity remains constant ( v = 2.0 m/s). That appears on the velocity-time graph as a horizontal line.

From 6.0 to 8.0 s - that is, for 6.0 s < t < 8.0 s - the acceleration is - 1.0 m/s2 . Then the velocity is given by

That is a straight line starting at v = 2.0 m/s and having a slope of - 1.0 m/s². That part of the velocity-time graph looks like this:

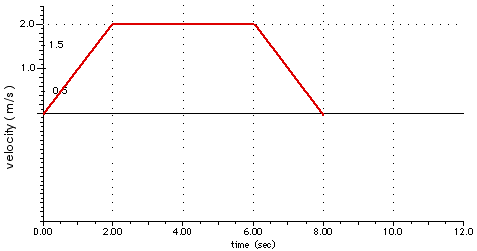
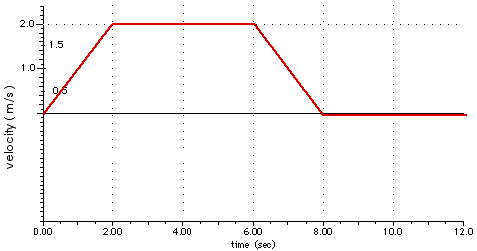
For the rest of the time, 8.0 s < t < 12.0 s, the acceleration is again zero so the velocity remains constant. During the two seconds from t = 6.0 s to 8.0 s, the velocity has been reduced from 2.0 m/s back to 0.0 so the object is at rest at 8.0 s. It remains at rest for the rest of the time.

Now, we will construct position-time graphs. As with the previous part, we will look at each time segment that has a constant acceleration. For 0 < t < 2.0 s, the acceleration was 1.0 m/s2 and the initial velocity was zero. Our position equation is

This is a curve-a parabola, actually-that starts at (x = 0, t = 0) and ends at (x = 2 m, t = 2 s). On a graph that looks something like this:

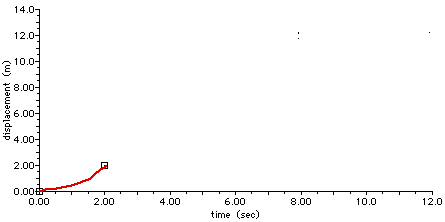
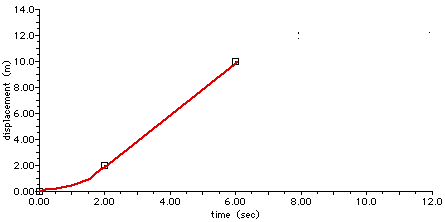
From 2.0 s to 6.0 s, the velocity remains constant at v = 2.0 m/s. This means the position, which is x = 2.0 m at time t = 2.0 s, increases at a steady, linear, constant rate.

We started this segment, at t_clock = 2.0 s, at a position of 2.0 m. At the end of the segment, with t_clock = 6.0 s, we are at position x = 10 m.

On a graph, that looks like this:

Now, at t = 6.0 s, there is a negative acceleration. At t = 6.0s, the velocity is 2.0 s; that becomes vi for this time segment. At t = 6.0 s, the position is 6.0 m; that becomes xi for this segment. For 6.0 s < t_clock < 8.0, we have a = - 1.0 m/s2 and the displacement equation becomes

At the end of this segment, for t = 8.0 s, the position (or displacement) is

[Be careful. I have written tclock = 8.0 s to keep track of our time overall. But our equations have all been developed with ti = 0 corresponding to xi and v, so the time that goes into this equation must be 2.0 s. If this is confusing, please let me know].

This means a curve on the graph that looks something like this:

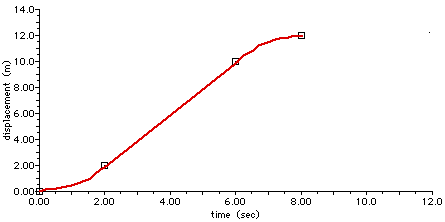
Now, for the final segment, with 8.0 s < t_clock < 12.0 s, the object remains at rest (v = 0) so the displacement remains constant, x = 12.0 m.

 

| ToC, Chapter 2 | Course Calendar |

 

(c) 2002, Doug Davis; all rights reserved