



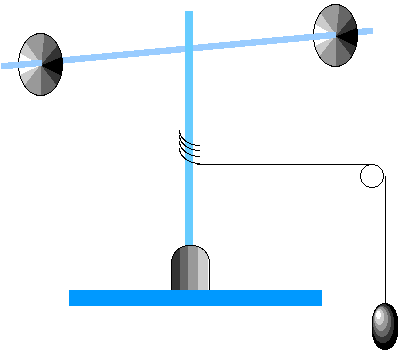
As always, begin with good force diagrams!First, draw all the forces on the hanging mass:
From that, we can apply Newton's Second Law. Since this mass is accelerating downward, let's take down as positive.
Fnet = m a Fnet = w - T = m a
1.47 N - T = (0.150 kg) a
This provides only one equation but there are two unknowns. So we need additional information. Look at the forces -- and torques -- on the rotating frame.
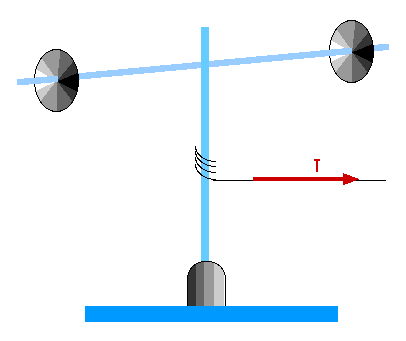
T is the tension in the string. This force is exerted perpendicular to the radius from the axis of rotation so it provides a torque (or "rotational force") of
= r F
= r T
= (0.0075 m) T
The rotational equivalent of Newton's Second Law is
= I
We know the value of I, the moment of inertia (or the "rotational mass");
I = 0.0080 kg m2
= I
(0.0075 m) T = (0.0080 kg m2)
Now we have two equations -- but we now have three unknowns! However,
the angular acceleration of the frame is easily and directly related to a the linear acceleration of the hanging mass. The string attached to the rotating frame is attached to the hanging mass so these two are related by
a = r or
= a / r
That means we can write
(0.0075 m) T = (0.0080 kg m2) (a/r) (0.0075 m) T = (0.0080 kg m2) (a/0.0075 m)
(0.0075 m) T = [(0.0080 kg m2) / (0.0075 m)] a
(0.0075 m) T = (1.067 kg m) a
T = [(1.067 kg m) / (0.0075 m)] a
T = (142 kg) a
And -- finally -- we have two equations with two unknowns!
1.47 N - T = (0.150 kg) a 1.47 N - [ (142 kg) a ] = (0.150 kg) a
1.47 N = (0.150 kg) a + (142 kg) a
1.47 N = (142.15 kg) a
(142.15 kg) a = 1.47 N
a = 1.47 N / 142.15 kg
a = 0.01 m/s2
(c) 2000, Doug Davis; all rights reserved.