



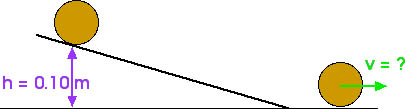
Consider a solid disk ( I = 1/2 M R2 ) that rolls down an inclined plane. The disk starts from rest and from a height of 0.10 m. It rolls down the inclined plane without slipping. What is its speed at the bottom of the plane?
(Be sure to include rotational Kinetic Energy).
Use Energy Conservation. The initial energy is the Potential Energy the disk has at the top of the inclined plane. The final energy is the sum of the translational Kinetic Energy and the Rotational Energy the disk has as it rolls along the level surface at the bottom of the plane.
KErot + KEtr = m g h
(1/2) I ![]() 2
+ (1/2) M v2 = M (10
m/s2) (0.10 m)
2
+ (1/2) M v2 = M (10
m/s2) (0.10 m)
Since it rolls without slipping, we also know
or
(1/2) [(1/2) M r2](v/ r)2 + (1/2) M v2 = M (10 m/s2) (0.10 m) = M (m2/s2)
(1/4) [ M r2][v2/ r2] + (1/2) M v2 = M (m2/s2)
(1/4) M v2 + (1/2) M v2 = M (m2/s2)
(3/4) M v2 = M (m2/s2)
(3/4) v2 = 1.0 (m2/s2)
v2 = (4/3) 1.0 (m2/s2)
v2 = 1.33 (m2/s2)
v = 1.15 (m/s)
(c) 2000, Doug Davis; all rights reserved.