Angular Momentum - 1
For linear motion, we found it very useful to describe motion in terms of the (linear) momentum,
Momentum was important because momentum is conserved. That is the total amount of momentum of a system is a constant.
In a similar manner, we will define the angular momentum L of an object as
L = I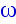 
Like linear momentum, angular momentum is
important -- and interesting! -- because angular momentum is
conserved! That means the value of the angular momentum
remains constant. We can often change the "rotational mass" or the
"moment of inertia". This will cause the angular velocity
to change to keep the angular momentul L at its original
value.
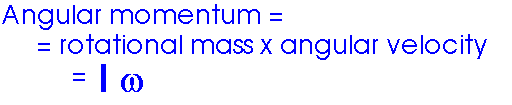
This can give a whole new meaning to the phrase "dizzy Physics professor".
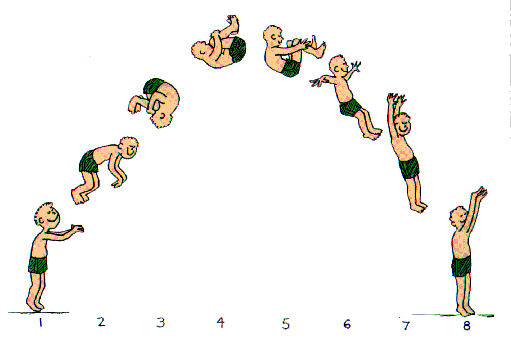
Remember conservation of angular momentum the next time you watch a gymnast, a diver, a ballerina, or an ice skater!
 |
 |
|
 |
|
|
|
||
|
|
|||