First Condition of Equilibrium

We may say that an object at rest is in equilibrium or in static equilibrium. An object at rest is described by Newton's First Law of Motion. An object in static equilibrium has zero net force acting upon it.

The First Condition of Equilibrium is that the vector sum of all the forces acting on a body vanishes. This can be written as

F = F₁+ F₂+ F₃+ F₄+. . . = 0

where , the Greek letter sigma, again means the summation of whatever follows -- the summation of the forces, in this case.

That's all there is!

However, remember the following

=>> Ensure that you have included all the forces. This means carefully draw a free body diagram. Include gravity (the weight) and all contact forces.

=>> Remember that forces are vectors.

That means that the first condition of equilibrium,

F = 0

really means

Fx = 0

Fy = 0

---

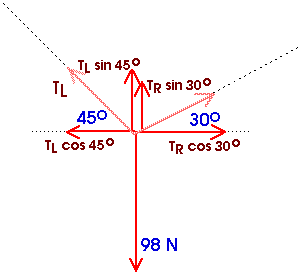
Example: Consider the 98 newton weight (or 10 kg mass) supported by a rope.

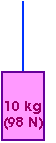
The tension in the rope attached to the 98 newton weight is just 98 newtons.

But this rope is now tied together with two other ropes as shown here.

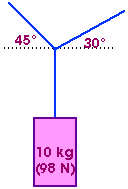
What forces are exerted by the other two ropes?

To answer this, look at the forces exerted on the knot where the three ropes are joined. The knot at rest so the sum of the forces acting on it must be zero.

Draw a free-body diagram showing just those forces.

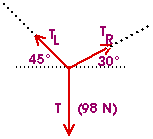
T is the magnitude of the force on the knot from the rope attached directly to the weight. T_L is the magnitude of the force on the knot from the rope on the left that makes an angle of 45° with the horizontal. And T_R is the magnitude of the force on the knot from the rope on the right that makes an angle of 30° with the horizontal. These three forces must add to zero. Graphically, they can be added as shown here; the force vectors form a closed triangle.

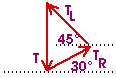
Now we apply the first condition of equilibrium,

F = 0

which really means

Fx = 0

Fy = 0

First, resolve all the forces into their x- and y-components.

Fx = 0 Fx = - TL cos 45o + TR cos 30o = 0 - 0.707 TL + 0.866 TR = 0 0.866 T R = 0.707 TL	Fy = 0 Fy = TL sin 45o + TR sin 30o - 98 N = 0 0.707 TL + 0.5 TR - 98 N = 0 0.707 TL + 0.5 TR = 98 N
Now we can substitute,
	0.707 TL + 0.5 TR = 98 N 0.866 T R + 0.5 TR = 98 N ( 0.866 + 0.5 ) TR = 98 N 1.366 TR = 98 N TR = 98 N / 1.366 TR = 71.7 N
0.866 T R = 0.707 TL TL = (0.866 / 0.707) TR TL = 1.22 TR TL = 1.22 ( 71.7 N ) TL = 87.8 N

ToC			Static Friction
Return ToC, Static Equilibrium

(c) 2002, Doug Davis; all rights reserved