Elastic Potential Energy

How much work is done when we stretch a spring a distance x from its equilibrium position?

First, we need to know about the general characteristics of a spring.

Experimentally, we find

This is known as Hooke's law

We might write this in equation form as F = k x. However, the force exerted by the spring is always in the opposite direction to the stretch (or compression) of the spring. Therefore, we write Hooke's law as

F = - k x

This is the force exerted by the spring. The external force we exert on the spring is F_ext = + k x.

The proportionality constant k is known as the spring constant and describes how stiff the spring is.

Now we are again ready to ask

"How much work is done when we stretch a spring a distance x from its equilibrium position?"

We know how to handle a constant force. For a constant force, we know

W = F d

Our spring force varies, but we can think of it as being (nearly) constant as we move through a (very) small distance,

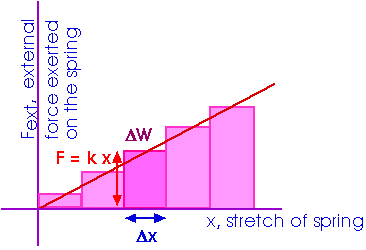
The work done by a variable force is the area under the "curve" on a Force - distance graph. For this Hooke's law force of F_ext = k x, the work done to the spring by the external force F_ext is

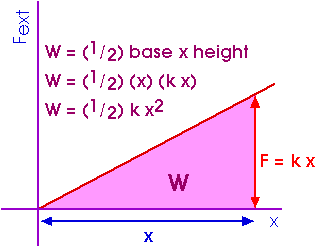
W = (¹/₂) k x²

This work done on the spring as it is stretched (or compressed) can be recovered. This is stored work that can be used to do work on something else by this spring. That means the stretched (or compressed) spring has energy -- potential energy. This is spring potential energy or elastic potential energy.

PE_el = (¹/₂) k x²

^or

U_el = (¹/₂) k x²

Gravitational Potential Energy			Energy Conservation
Return to ToC, Work and Energy

(c) 2002, Doug Davis; all rights reserved