Uniform Circular Motion (UCM)
Consider an object moving along a circular path with constant or uniform speed. This might be a guest on a carousel at an amusement park, a child on a merry-go-round at a playground, a car with lost driver navigating a round-about or "rotary", a yo-yo on the end of a string, a satellite in a circular orbit around Earth, or Earth in its (nearly) circular orbit around out Sun.
As an object travels in a circle, the direction of its velocity changes. Even tho' the speed remains univorm, the velocity changes because its direction changes.
v = v2 - v1
This is not zero, even tho'
| v2 | = v2 = | v1 | = v1 = v v is the speed, which remains constant. You can see
Notice the two similar triangles in the position vectors and the velocity vectors,
or
or
Since these are similar triangles,we know that
For small changes in time or for small angles
, the distance
This means
ac = v2 / r
Angular velocityHow fast is something turning or rotating or revolving? We call this its angular velocity and give it the symbol
, the lower case Greek letter omega. It may have units of revolutions per minute or revolutions per second or, better yet, radian per second.
Most of us are comfortable measuring an angle in degrees. But measuring an angle in radians is usually more useful.
While we can measure the angle
Such a definition means this measure of the angle has no dimensions. We have taken an arc length, measured in something like meters, and divided it by a radius, also measured in something like meters. However, since we expect dimensions or units, we call this unit of angular measure a radian. You may think of radians as added for cosmetic purposes! How large is a radian?
Consider a complete circle. We would describe a complete circle as having an angle of 360o. In terms of radians, a complete circle has an arc length equal to its circumference, s = C = 2
r.
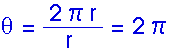
What does all this have to do with uniform circular motion? The arc length traveled by a point on a rotating object is equal to the radius of that point multiplied by the angle
s = r when
That means the linear speed v of a point on a rotating object is equal to the radius of that point multiplied by the angular speed
v = r provided
Example
An audio CD rotates at 150 rpm (revolutions per minute). What is the linear speed of a small scratch on the CD that is 10 cm from the center?
v = r v = (10 cm) (150 rev/min) [ 2
v = 157 cm / s
Example
Calculate the centripetal acceleration of our moon.
It is in a nearly circular orbit of radius r = 3.84 x 108 m and has a period of 27.32 days.
Our moon moves in a circle so its direction changes continually; that means it has an acceleration because its velocity changes; this is the centripetal acceleration. From its radius and period we can find its speed and then calculate its centripetal acceleration.
ac = v2 / r First we must find its speed v from the total distance traveled D divided by the time required T,
D = 2 v = D / T
v = 2
v = [2(3.14) ( 3.84 x 108 m ) ]/ (27.32 da)][da/24h][h/3600s]
v = 1 022 m / s
ac = v2 / r
ac = (1 022 m / s)2 / 3.84 x 108 m
ac = 2.72 x 10-3 m / s2 = 2.72 mm / s2
Example
A rubber ball with mass of 50 grams is attached to a string one meter in length. What is the tension in the string if the ball moves in a circle on a horizontal, frictionless table with a constant speed of 4.2 m/s?
The vertical forces--the downward force of gravity (or weight) and the upward normal force of the table--cancel each other. The tension in the string provides the net force on the moving rubber ball. That net force causes the ball to move in a circle; it is the centripetal force, Fc = m v2 / r.
This is a direct application of F = m a since the tension in the string is the net force which is also the centripetal force,
Fc = m v2 / r Fc = ( 0.050 kg ) ( 4.2 m / s )2 / (1.0 m)
Fc = 0.88 N
(c) 2002, Doug Davis; all rights reserved
UCM Examples Curves Return to ToC, UCM & Gravity
