

Coordinate Systems and Reference Frames
A point can be located on an x-, y- coordinate system by its coordinates x and y.
The x-coordinate describes how far along the x-axis the point is located while the y-coordinate describes how far along the y-axis the point is located.
The x- and y-coordinates may be either positive or negative as seen in the examples above.
We will use bold face type to indicate a vector, such as r. In writing a vector by hand, we will indicate that something is a vector by drawing an arrow above it as
. Some such distinguising notation is important. Do not write a vector without some distinguishing characteristic or notation.
We can describe the point (x,y) as a point located by a vector r that has components of x and y.
We can call this x-component, a vector along the x-direction of length x, and indicate that it is a vector by x or
. Likewise, we can call this y-component, a vector along the y-direction of length y, and indicate that it is a vector by y or
. Then we can write
r = x + y or
=
+
Please note that it is _not_ true to write r = x + y.
r is the length of the vector or the magnitude of the vector. The angle
(theta) gives the direction of the vector. How are r, x, y, and
related?
Notice that r, x, and y form the sides of a right triangle. Right triangles are special because of their relation with the trigonometry functions.
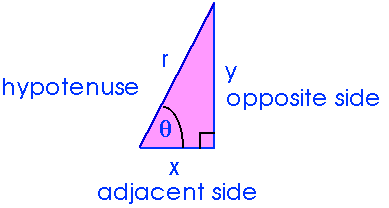
If we know r, x, and y we can find the trig functions for the angle
. More likely, tho', is the situation where we know x and y and want to find r and
. Or we may know r and
and want to find x and y. All those situations can be handled with the trig functions.
It is common practice to measure the angle
from the positive x-axis and to measure it positive for a counter-clockwise direction. The example shown below might be for an angle of
= 53o. Then, if r = 10, the components will be
x = r cos = (10) (0.6) = 6
y = r sin
= (10) (0.8) = 8
Please do not memorize these equations. Remember the more basic definitions of the trig functions,
sin = opp / hyp
cos
= adj / hyp
tan
= opp / adj
Then, for this particular case of measuring angle
from the x-axis, we have
r = hyp x = adj
y = opp
and that means that
sin = y / r
cos
= x / r
tan
= y / x
or
x = r cos 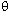
y = r sin
Of course, angle
does not need to be limited to the first quadrant. Below might be a diagram for
= 150o. Again, let r = 10 for this numerical example. For that case,
x = r cos = (10) ( cos 150o) = (10) ( - 0.866) = - 8.66
y = r sin
= (10) ( sin 150o) = (10) ( 0.500) = 5.00
Notice the signs and compare them with the diagram. x = - 8.66 is located to the left and y = + 5.00 is located up. Always make a diagram! And then compare your results - your answers - with your diagram. Signs are vital and it is all too easy to drop them and simply use the magnitudes.
The diagram below might be for r = 10 and
= 210o. For those values, we can find the components by
x = r cos = (10) ( cos 210o ) = (10) ( - 0.866) = - 8.66
y = r sin
= (10) ( sin 210o ) = (10) ( - 0.500) = - 5.00
Again, notice the signs and compare them with the diagram. x = - 8.66 is located to the left and y = - 5.00 is located down. Always make a diagram! And then compare your results - your answers - with your diagram. Signs are vital and it is all too easy to drop them and simply use the magnitudes.
We can describe this vector as r = 10,
= 210o as we have above. Or, we can measure angle
clockwise as we have below and describe this vector as r = 10,
= - 150o. Either description is as good as the other. They are two ways of describing the same vector or the same point.
While it is common to measure angles from the x-axis and to measure them as positive if they are counter-clockwise, it is _not_ necessary to do so. Airplane pilots commonly measure angles or directions from North (y) and measure them as positive for clockwise angles. Below might be a location or a vector of r = 10 km,
= 53o. In this case, we have
x = r sin = (10 km) (sin 53o) = (10 km) (0.8) = 8 km
y = r cos
= (10 km) (cos 53o) = (10 km) (0.6) = 6 km
Notice that for this arrangement, x is now the opposite side (the side of the right triangle opposite the angle
) and y is now the adjacent side (the side of the right triangle adjacent to the angle
). If you always start with the basic definitions of sine and cosine, you will not have a problem.
Giving a location or a vector in terms of the coordinates (x, y) means we are using a cartesian coordinate system (or reference frame).
Giving a location or a vector in terms of the coordinates (r,
) means we are using a polar coordinate system (or reference frame).
ToC, Vectors Vectors and Scalars Return to ToC, Vectors and 2D Motion (c) 2002, Doug Davis; all rights reserved