PHY 1150
Chapter 13; Oscillations about Equilibrium

| Return to Calendar |

D13.1 Find the frequency of a mass on a spring oscillator with the following values for the mass and the spring constant:
mass (kg)
spring constant ( N / m )

a
1.0
2.5
b
2.5
1.0
c
3.0
7.2
d
50
100
e
80
200
f
100
250
g
120
250
h
200
500

This is an excellent one to solve with a spreadsheet.

D13.2 Find the frequency of the oscillator in this arrangement with the mass attached between two springs of spring constants k 1 and k 2.

 

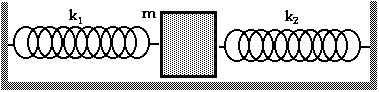
The next arrangement of springs is a little more "tricky" or more interesting. Find the frequency of the oscillator in this arrangement with the mass attached to two springs of spring constants k 1 and k 2 as shown in the diagram here.

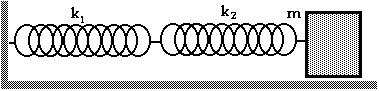
And with this third arrangement, again, find the frequency of the oscillator with the mass attached to two springs of spring constants k 1 and k 2 as shown in the diagram here.

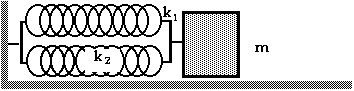
D13.3 How much work is done when a spring with spring constant 80 N/m is stretched 0.15 m (or 15 cm)?

D13.4 Consider, as a simple harmonic oscillator, a 200 g (0.20 kg) mass attached to spring with a spring constant of 50 N/m. If the oscillator has an amplitude of 10 cm (0.1 m), what is the maximum speed of the mass?

D13.5 An object undergoes simple harmonic motion with an amplitude of 12 cm. At a point 8.0 cm from equilibrium, its speed is 20 cm/s. What is the period?

Caution: be very careful with the units!

D13.6 For each of the simple harmonic oscillators listed in the table below, find the velocity of the mass at the position given:

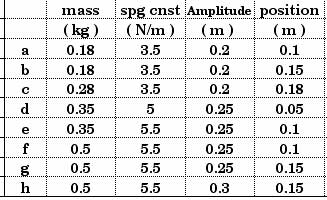
These multiple-data-set problems are good ones to solve with a spreadsheet. This is basically energy conservation.

D13.7 A 50-g (0.050 kg) mass hanging from a spring oscillates with a frequency of 2 Hz. What is the spring constant?

| Return to Calendar |

(c) 2005, Doug Davis; all rights reserved