
Chapter 11; Rotational Dynamics and Static Equilibrium
![]()
| ToC, Chapter 11 | Course Calendar |
![]()

Chapter 11; Rotational Dynamics and Static Equilibrium
![]()
| ToC, Chapter 11 | Course Calendar |
![]()
D11.1 A solid, uniform cylinder of 12 cm radius with mass of 5.0 kg is free to rotate about its symmetry axis. A cord is wound around the drum and a 1.2 kg mass is attached to the end of the cord. Find the acceleration of the hanging mass, the angular acceleration of the cylinder, and the tension in the cord.
D11.2 A 10 kg block sits on a horizontal surface with coefficient of friction of 0.2 between the block and the surface. A string runs from this block over a wheel of radius 10 cm and moment of inertia of 2.0 kg m2 and is attached to a hanging 5 kg mass. Find the acceleration of the masses, the angular acceleration of the wheel, and the tension in the string on each side.
D11.3 Assume a playground merry-go-round to be a uniform cylinder or disk of 150 kg and 1.8 m radius. What is its moment of inertia?
It is initially at rest when a 50 kg child, running at 4 m/s, in a direction tangential to the edge of the merry-go- round, jumps on. What is its angular velocity after the child sits down on the edge?
D11.4 A basket of tomatoes of mass 20.0 kg is being hoisted by a windlass. The rope is wrapped around an axle that is a solid cylinder of wood having a radius of 0.1 m and a mass of 10 kg. The mass of the crank handles is neglibible. The operator lets go of the handle when the basket is 6 m above the ground. With what linear speed does the basket strike the ground?
D11.5 To demonstrate conservation of angular momentum a Physics professor stands on a frictionless turntable with a 2 kg mass in each outstretched hand. An assistant gives her a small initial angular velocity of 2 rad/s. She then drops her hands to her sides and her angular velocity increases dramatically. As a rough estimate, consider her arms to have mass of 5 kg each and to be 1 m long rods hinged at the axis of rotation. The rest of her body has an approximate moment of inertia of 0.55 kg m2. Find her final angular velocity when the masses are 0.25 m from the axis of rotation. Calculate the initial and final values of the rotational kinetic energy and explain the cause of the difference in these values.
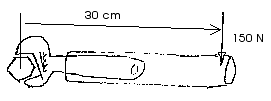
D11.6 A piece
of pipe may sometimes be used as a "cheater" to effectively lengthen the moment
arm of a wrench. If a pipe is used as shown in the figure to allow a 150 N force
to be exerted 30 cm from the bolt, what torque is exerted on the bolt?
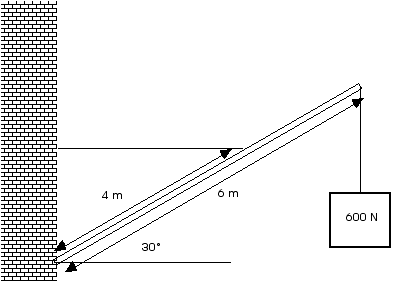
D11.7 A lightweight,
uniform pole is 6 m long and is attached by a pivot at one end to a wall. The
pole is held at an angle of 30° above the horizontal by a horizontal guy
wire attached to the pole 4.0 m from the end attached to the wall. A load of 600
N hangs from the upper end of the pole. Find the tension in the guy wire and the
components of the force exerted on the pole by the wall.
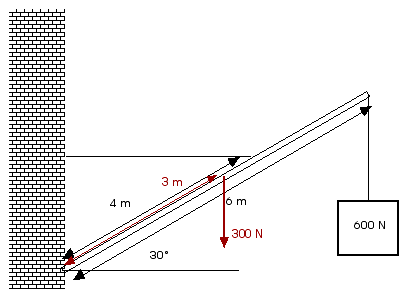
D11.8 A uniform pole 6 m long weighs 300 N and is attached by a pivot at one end to a wall. The pole is held at an angle of 30° above the horizontal by a horizontal guy wire attached to the pole 4.0 m from the end attached to the wall. A load of 600 N hangs from the upper end of the pole. Find the tension in the guy wire and the components of the force exerted on the pole by the wall.
(Compare this to the previous question, D11.7).
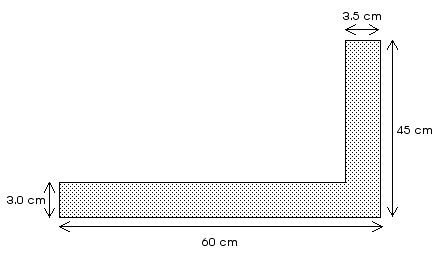
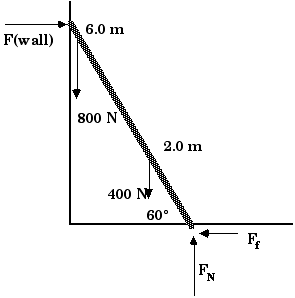
D11.9 A carpenter's square has the dimensions shown in the figure. It is made of uniformly thick metal. Locate its center of gravity or center of mass.
![]()
![]()
(C) 2005; Doug Davis, all rights reserved.