Chapter 11; Rotational Dynamics and Static Equilibrium

| ToC, Chapter 11 | Course Calendar |

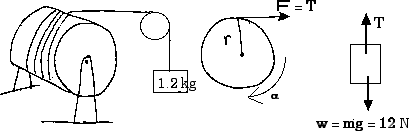
For the 1.2 kg mass, take down as positive and apply Newton's Second Law,

For the rotating cylinder, apply the rotational form of Newton's Second Law,

_net = I
_net = r F sin
_net = (0.12 m) (T) (1)

since = 90°

For a solid cylinder,

I = M r²
I = (0.5) (5.0 kg) (0.12 m)²
I = 0.036 kg m²

Therefore,

_net = (0.12 m) T = (0.036 kg m²) a

At the moment, we have three unknowns, T, a, and , in two equations. The angular acceleration of the cylinder and the linear acceleration of the cord or of the hanging mass are connected by

a = r
a = (0.12 m)
= a / 0.12 m

(0.12 m) T = (0.036 kg m²) a / 0.12 m
T = (0.036 kg m²) a / (0.12 m)²
T = (2.5 kg) a

Now we have two equations in two unknowns

12 N - T = (1.2 kg) a
12 N - (2.5 kg) a = (1.2 kg) a
12 N - (2.5 kg) a = (1.2 kg) a
12 N = (3.7 kg) a
a =
a = 3.24

T = 8.1 N

D11.2 A 10 kg block sits on a horizontal surface with coefficient of friction of 0.2 between the block and the surface. A string runs from this block over a wheel of radius 10 cm and moment of inertia of 2.0 kg m² and is attached to a hanging 5 kg mass. Find the acceleration of the masses, the angular acceleration of the wheel, and the tension in the string on each side.

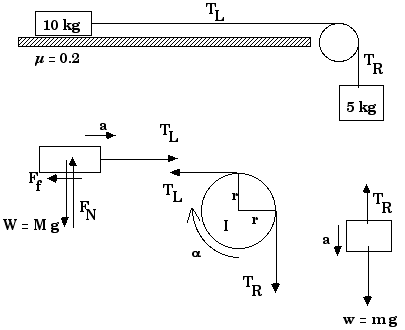
Notice that the tension is different on the two sides of the pulley because the pulley is (very) massive.
For the 10-kg block on the horizontal plane, we can write

and

We can use this information to determine the friction force,

Then the F_net,x equation becomes

For the massive pulley, we have

_net = r T_R - r T_L = (0.10 m) T_R - (0.10 m) T_L
net = I = (10 kg m²)
(0.10 m) T_R - (0.10 m) T_L = (2.0 kg m²)

We now have four unknowns -- T_L, T_R, a, and -- in two equations. The angular acceleration of the cylinder and the linear acceleration of the cord or of the hanging mass are connected by

a = r
a = (0.10 m)
= a / 0.10 m
(0.10 m) T_R - (0.10 m) T_L = (2.0 kg m²)
(0.10 m) T_R - (0.10 m) T_L = (2.0 kg m²) a / 0.10 m
T_R - T_L = (2.0 kg m²) a / (0.10 m)²

T_R - T_L = (200 kg) a

We now have three unknowns --T_L, T_R, and a -- in two equations. We still must apply Newton's Second Law to the hanging mass. There we may as well take down as positive,

Now we have three equations for three unknowns,

T_L = 20 N + (10 kg) a
T_R - T_L = (200 kg) a
50 N - T_R = (5 kg) a

T_R - [20 N + (10 kg) a] = (200 kg) a
T_R = 20 N + (190 kg) a

50 N - [20 N + (190 kg) a] = (5 kg) a
30 N = (195 kg) a
a = = 0.15
a = 0.15
= a / 0.10 m = 1.5
T_L = 20 N + (10 kg) a = 20 N + 1.5 N = 21.5 N

T_R = 20 N + (190 kg) (0.15 ) = 49.2 N

D11.3 Assume a playground merry-go-round to be a uniform cylinder or disk of 150 kg and 1.8 m radius. What is its moment of inertia?

It is initially at rest when a 50 kg child, running at 4 m/s, in a direction tangential to the edge of the merry-go- round, jumps on. What is its angular velocity after the child sits down on the edge?

For a solid disk or cylinder,

I_disk = M r²

Therefore, the moment of inertia of the merry-go-round is

I_disk = (150 kg)(1.8 m)² = 243 kg m²

The initial angular momentum of the child is

The initial angular momentum of the merry-go-round is zero.
So the total initial angular momentum of the entire system is

If the bearings of the merry-go-round are well oiled this should be the total final angular momentum,

L_final = 360 kg m²/s
L_final = I

but now the moment of inertia is the moment of inertia of the merry-go-round and the child

I_child = m r² = (50 kg)(1.8 m)² = 162 kg m²
I_total = I_disk + I_child = 243 kg m² + 162 kg m²
I_total = 405 kg m²
L_final = I = (405 kg m²) = L_initial
(405 kg m²) = 360 kg m²/s
= 0.89

D11.4 A basket of tomatoes of mass 20.0 kg is being hoisted by a windlass. The rope is wrapped around an axle that is a solid cylinder of wood having a radius of 0.1 m and a mass of 10 kg. The mass of the crank handles is neglibible. The operator lets go of the handle when the basket is 6 m above the ground. With what linear speed does the basket strike the ground?

The moment of inertia for a solid cylinder (or a disk) is

The velocity of the load and the angular velocity of the windlass are connected by

v = r
v = (0.1 m)
= ^v/_{0.1 m}

As always, good diagrams make life much simpler.

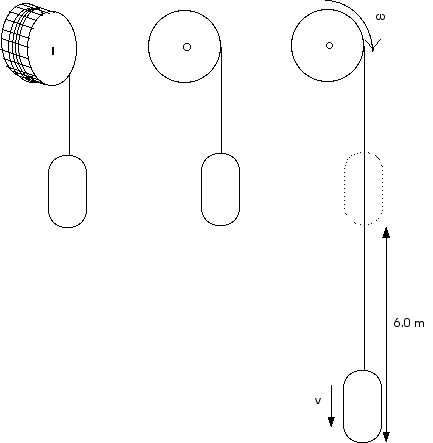
Initially, before the windlass and load are released, we have

In this problem, as in the previous one, the Kinetic Energy of the wheel or drum or cylinder is far greater than the Kinetic Energy of the masses and dominates the entire motion.
Finally, after the windlass has increased its angular speed and the load has increased its linear speed, and just before the load hits the floor, we have

KE_tr,f = (¹/₂) m v² = (¹/₂) (20 kg) v² = 10 kg v²
KE_rot,f = (¹/₂) I ² = (¹/₂) (0.05 kg m²) ² = (¹/₂) (0.05 kg m²) (^v/_{0.1 m})² =
KE_rot,f = (2.5 kg) v^2
KE_tot,f = (12.5 kg) v²
PE_f = 0
E_tot,f = (12.5 kg) v²= 1,176 J = E_tot,i
(12.5 kg) v²= 1,176 J
v² = ^{1,176 J} / _{12.5 kg}
v² = 94.1 m²/s²
v = 9.7 m/s
v = 9.7 m/s

D11.5 To demonstrate conservation of angular momentum a Physics professor stands on a frictionless turntable with a 2 kg mass in each outstretched hand. An assistant gives her a small initial angular velocity of 2 rad/s. She then drops her hands to her sides and her angular velocity increases dramatically. As a rough estimate, consider her arms to have mass of 5 kg each and to be 1 m long rods hinged at the axis of rotation. The rest of her body has an approximate moment of inertia of 0.55 kg m². Find her final angular velocity when the masses are 0.25 m from the axis of rotation. Calculate the initial and final values of the rotational kinetic energy and explain the cause of the difference in these values.

I_body = 0.55 kg m²
I_rod = M l²
I_{arms, out} = 2 [ (5 kg)(1 m)² ] = 3.33 kg m²
I_{wts, out} = 2 [ (2 kg) (1 m)² ] = 4 kg m²
I_{total, initial} = (0.55 + 3.33 + 4) kg m² = 7.88 kg m²

The initial angular momentum is

L_initial = I_{initial initial}
L_initial = (7.88 kg m²) (2 ) = 15.76
KE_initial = I ² = (7.88 kg m²)(2 )²
KE_initial = 15.75 J

(It is only a coincident that L and KE happen to have the same numerical value!).
As she pulls in her hands, the total moment of inertia changes,

I_body = 0.55 kg m²
I_{arms, in} = 2 [ (5 kg)(0.25 m)² ] = 0.21 kg m²
I_{wts, in} = 2 [ (2 kg) (0.25 m)² ] = 0.25 kg m²
I_{total, final}=(0.55 + 0.21 + 0.25) kg m² = 1.01 kg m²

Total angular momentum is conserved,

L_final = L_initial
L_final = I_{final final} = 15.76 = L_initial
(1.01 kg m²) _final = 15.76
_final = 15.6
KE_final = I ² = (1.01 kg m²)(15.6 )²
KE_final = 123 J

Work must be done on the weights to pull them in toward the axis of rotation. This work that is done by the dizzy professor shows up as increased kinetic energy.

D11.6 A piece of pipe may sometimes be used as a "cheater" to effectively lengthen the moment arm of a wrench. If a pipe is used as shown in the figure to allow a 150 N force to be exerted 30 cm from the bolt, what torque is exerted on the bolt?

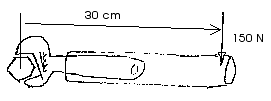
= r F sin
= (0.30 m) (150 N) (1)
= 45 m-N

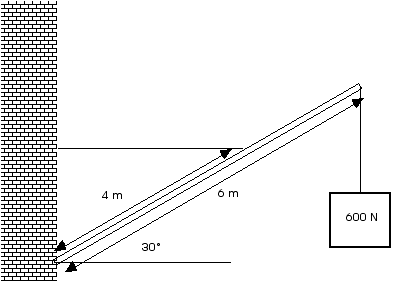
As always, a free body diagram or a force diagram is essential.

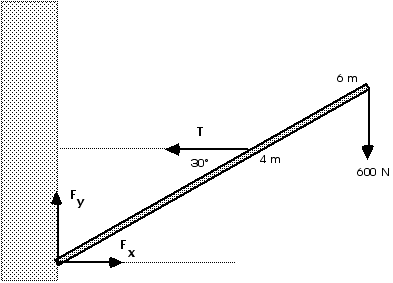
From the first condition of equilibrium, we have

F = 0

But that really means

Fx = 0	and	Fy = 0
Fx = Fx - T = 0		Fy = Fy - 600 N = 0
Fx = T		Fy = 600 N

More information is needed to solve for T and F_x. We can get that information from the second condition of equilibrium. Before we start to calculate torques, we must decide on the reference point about which we will calculate those torques. If we choose the lower, left end of the pole, there are two forces, F_x and F_y, that will have zero torque. That will reduce the number of terms in all of our equations. Therefore, that is a good choice for the origin or reference point or axis of rotation.

Therefore,

And we already knew

D11.8 A uniform pole 6 m long weighs 300 N and is attached by a pivot at one end to a wall. The pole is held at an angle of 30° above the horizontal by a horizontal guy wire attached to the pole 4.0 m from the end attached to the wall. A load of 600 N hangs from the upper end of the pole. Find the tension in the guy wire and the components of the force exerted on the pole by the wall.

(Compare this to the previous question, D11.7).

Don't forget the 300 N weight of the pole itself!!!

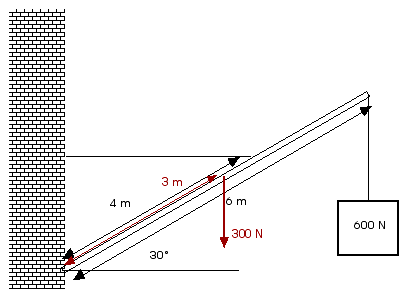
As always, a good free body diagram is essential!

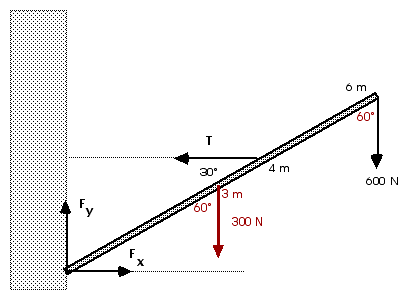
From the first condition of equilibrium, we have

F = 0

But that is a vector equation so it really means

Fx = 0	and	Fy = 0
Fx = Fx - T = 0		Fy = Fy - 600 N - 300 N = 0
Fx = T		Fy = 900 N

More information is needed to solve for T and F_x. We can get that information from the second condition of equilibrium. Before we start to calculate torques, we must decide on the reference point about which we will calculate those torques. If we choose the lower, left end of the pole, there are two forces, F_x and F_y, that will have zero torque. That will reduce the number of terms in all of our equations. Therefore, that is a good choice for the origin or reference point or axis of rotation.

Therefore,

And we already knew

F_y = 900 N

---

D11.9 A carpenter's square has the dimensions shown in the figure. It is made of uniformly thick metal. Locate its center of gravity or center of mass.

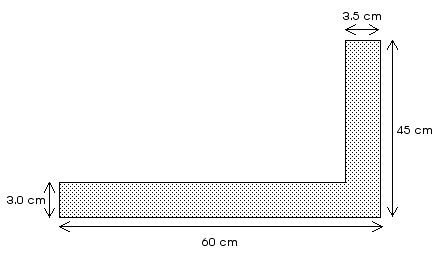
Think of the square as being made of two rectangles.

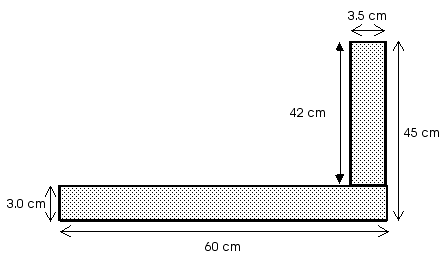
The center of gravity of each rectangle is at the geometric center of that rectangle and the mass (or weight) located at that position is proportional to the area of that rectangle.

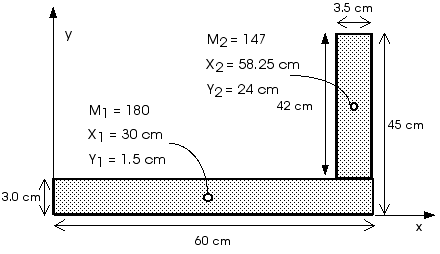
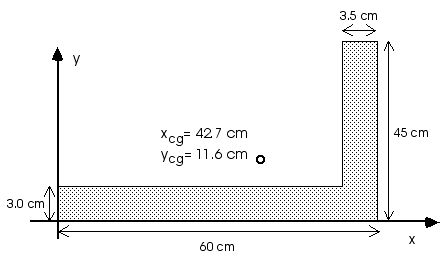
Notice that the positions are all measured from the lower left corner of the carpenter's square. Now we can use the defintions of center of gravity, Equations 8.10 and 8.11, to locate the center of gravity of the entire object,

---

D11.10 Ladder problems are fun. Ladder problems are classic. A ladder problem will surely reappear on an hour exam or the final.

A man who weighs 800 N climbs to the top of a 6 meter ladder that is leaning agains a smooth (ie, frictionless) wall at an angle of 60° with the horizontal as sketched in the figure below. The non-uniform ladder weighs 400 N and its center of gravity is 2 meters from the foot of the ladder. What must be the minimum coefficient of static friction between the ground and the foot of the ladder if it is not to slip? 

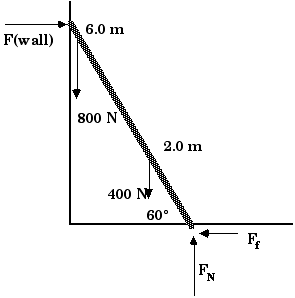
Using the first condition of equilibrium, we have

F_x = F_wall - F_f = 0

F_wall = F_f

and

F_y = F_N - 400 N - 800 N = 0

F_N = 1200 N

To solve for F_wall and, thus, for F_f, we must use the second condition of equilibrium. In calculating the torques, let us calculate torques about the foot of the ladder. That choice means two of the forces, F_N and F_f , will provide zero torque and that reduces the number of terms in our equations. Be very careful of the angles!

= r F sin

F_wall: _cw = (6.0 m)(F_wall)(sin 60°) = (6.0 m)(F_wall)(0.866)

_cw = (5.2 m) F_wall

800 N: _ccw = (6.0 m)(800 N)(sin 30°) = 2400 m-N
400 N: _ccw = (2.0 m)(400 N)(sin 30°) = 400 m-N

F_wall : = 0
F_f : = 0

_cw = _ccw
(5.2 m) F_wall = 2400 m-N + 400 m-N
(5.2 m) F_wall = 2800 m-N
F_wall = 538 N
F_f = 538 N

µ = 0.45

| Return to Calendar |

(C) 2005; Doug Davis, all rights reserved.

| Return to Calendar |

(c) 2005, Doug Davis; all rights reserved .