PHY 1151

Chapter 8; Potential Energy & Conservative Forces

 

| ToC, Chapter 8 | Course Calendar |

 

D8.1 A ski slope drops at an angle of 20° and is 600 m long. Find the change in potential energy of a 70-kg skier who goes down this slope.

PE = m g h = (70 kg)(9.8 m/s2)(205 m) = 141,000 J = 141 kJ

D8.2 In loading a certain dart gun, the dart is pushed in 12 cm before the gun is cocked. A force of 20 N is required at the end. Find the spring constant of the spring in the gun. Find the total amount of energy stored in the spring.

F = k x
k = = = 167
PEel = (1/2) k x2
PEel = (1/2) (167 N/m)(0.12 m)2
PEel = 1.2 J

D8.3 An arrow of mass 0.1 kg is fired directly upward by an archer who exerts an average force of 75 N on a bowstring that is pulled back 0.6 m. After it comes down, the arrow penetrates 20 cm vertically into the ground. Use the ideas of work and energy to answer the following:

a) With what speed does the arrow leave the bow?
b) How high does the arrow go?
c) What average upward force does the ground exert on the arrow while stopping it?


a)

Ef = (1/2) m v2 = Ei = W = (75 N)(0.6 m) = 45.00 J

(1/2) (0.1 kg) v2 = 45.0 J
v2 = 900 m2/s2
v = 30 m/s

 

b)
Ef = m g h = 45 J
(0.1 kg) (9.8 m/s2) h = 45 J
h = 45.9 m

c)

W = F D = 45.0 J
F (0.2 m) = 45.0 J
F = 225 N

D8.4 A ball is attached to a cord of length L which is initially held horizontal from a fixed support at P as sketched in the figure. The ball is released from rest at point A.

a) Find its speed at point B, the bottom of the swing.
A peg is fixed at point O, a distance y directly below point P. The cord hits the peg and the ball swings upward in an arc as shown.
b) Find the ball's speed at point C when the cord between it and the peg is horizontal.
c) Find the ball's height (relative to its starting position) at point D, the top of its swing after hitting the peg (Assume y > L/2).
d) Find the ball's speed at point D, the top of its swing after hitting the peg.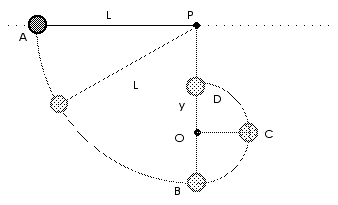

a) At position A, vA = 0 or KEA = 0
If we measure all the vertical distances from yB = 0 at position B, then at A, the mass has a height yA = L, so that

PEA = m g yA = m g L

( This choice for yB = 0 means PEB = 0 ).

Therefore, the total energy at A, EA, is

EA = KEA + PEA = 0 + m g L = m g L

Energy is conserved so

EB = EA
KEB = (1/2) m vB2
PEB = m g yB = 0

Remember, we have measured vertical distances here so we have set yB = 0. That means our total energy at position B is

EB = KEB + PEB = (1/2) m vB2 + 0 = (1/2) m vB2
EB = (1/2) m vB2 = m g L = EA
vB2 = 2 g L
vB =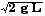

A peg is fixed at point O, a distance y directly below point P. The cord hits the peg and the ball swings upward in an arc as shown.
c) At position C, the (vertical) height above position B is

yC = (L - y)

Energy is conserved so

EC = EA
KEC = m vC2
PEC = m g yC = m g (L - y)

That means our total energy at position C is

EC = KEC + PEC = (1/2) m vC2 + m g (L - y)
EC = (1/2) m vC2 + m g (L - y) = m g L = EA
(1/2) m vC2 + m g L - m g y = m g L
(1/2) m vC2 = m g y
vC2 = 2 g y
vC =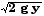

d) At position D, the (vertical) height above position B is

yD = 2 (L - y)

as can be seen by taking a more careful look at the diagram.
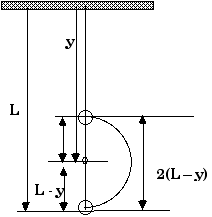
Energy is conserved so
ED = EA
KED = (1/2) m vD2
PED = m g yD = m g [2 (L - y)]

That means our total energy at position D is

ED = KEC + PEC = (1/2) m vC2 + m g [2 (L - y)]
ED = (1/2) m vD2 + m g [ 2 (L - y) ] = m g L = EA
(1/2) m vD2 + 2 m g L - 2 m g y = m g L
(1/2) m vD2 = 2 m g y - m g L
vD2 = 2 g ( 2 y - L )
vD =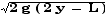

 

| ToC, Chapter 8 | Course Calendar |

 

(c) 2005, Doug Davis; all rights reserved.