
PHY 1151
Doug Davis

PHY 1151
Doug Davis
Ch 6, Applications of Newton's Laws
Friction
Translational Equilibrium
Circular Motion
![]()
| ToC, Chapter 6 | Course Calendar |
![]()
(Friction)
D6.1 A 7-kg package sits on a rough but level floor. The coefficient of sliding friction between the package and the floor is 0.27. A cord is attached to the package and makes an angle of 30° above the horizontal. What must be the tension in the cord to move the package along the surface with an acceleration of 1.0 m/s2?
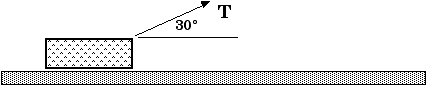
We must look at all the forces on the package. That means a carefully drawn free-body diagram.
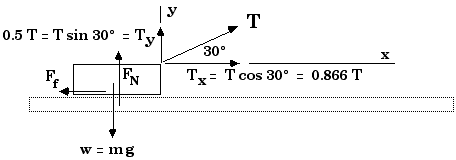
Now we can apply Newton's Second Law -- in its component forms -- to this situation.
Fnet,x = Tx - Ff = m ax = m a 0.866 T - Ff = (7.0 kg) a
0.866 T - Ff = (7.0 kg) (1.0 m/s2)
0.866 T - Ff = 7.0 N
We know the friction force only as
Ff = µ FN = 0.27 FN so we must solve for the normal force FN. We can do this by looking at the y-component of Newton's Second Law,
Fnet,y = Ty + FN - m g = m ay = 0 0.5 T + FN - (7.0 kg)(9.8 m/s2) = 0
0.5 T + FN - 68.6 N = 0
Now we have our required two equations since we have two unknowns (FN as well as T).
0.5 T + FN - 68.6 N = 0 FN = 68.6 N - 0.5 T
0.866 T - 0.27 (68.6 N - 0.5 T) = 7.0 N
0.866 T + 0.135 T = 7.0 N + 18.5 N
T = 25.5 N
D6.2 A man pushes a 20-kg lawn mower at constant speed with a force of 80 N directed along the handle, which makes an angle of 37° with the horizontal. Calculate the following:a) the horizontal and vertical components of the man's force.b) the horizontal retarding force on the mower.
c) the normal force between the mower and the lawn (be sure to include the mower's weight).
d) the effective coefficient of friction in this case.
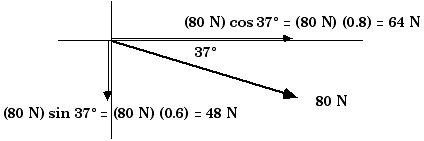
Fx = 64 N
Fy = - 48 N
(the negative sign meaning "down").
b) If the lawn mower moves at constant speed then the net horizontal force on it must be zero so the horizontal retarding force must be 64 N.
c) The net vertical force is zero,
Fnet,y = FN - m g - 48 N = 0 FN - (20 kg) (9.8 m/s2) - 48 N = 0
FN = 196 N + 48 N
FN = 144 N1/2
d) Ordinarily we describe the friction force in terms of
Ff = µ FN or
µ = Ff / FN If we consider the horizontal retarding force an effective friction force, then this becomes
µ = 64 N / 144 N = 0.44 µ = 0.44
(Translational Equilibrium)
D6.3 A 2-kg ball is held in position by a horizontal string and a string that makes an angle of 30° with the vertical, as shown in the figure. Find the tension T in the horizontal string.
F = 0
(Since I am writing this all in bold to begin with, it is difficult or impossible to explicitly tell that this is a vector equation--but it is! And that's very important!)
F = 0
But that really means
Fx = 0
and Fy = 0
Fx = - T + Tr cos 60° = 0
Fy = Tr sin 60° - 20 N = 0
- T + Tr (0.500) = 0 Tr (0.866) - 20 N = 0 T = Tr (0.500) Tr (0.866) = 20 N Tr = 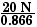
Tr = 23.1 N T = (23.1 N)(0.500) T = 11.5 N
D6.4 The pulleys shown in the figure below are frictionless but have a mass of 4 kg each. What is the tension in the cord and in the pulley supports?
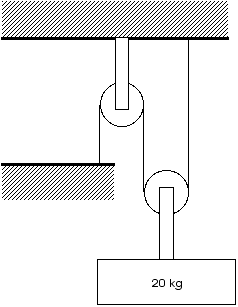
Apply the first condition of equilibrium to each pulley.
First to the one one the left,F = 0
F = S - T - 40 N - T = 0
S - 2 T = 40 NThat gives two unknowns in one equation so we must seek additional information. Of course, that will come from looking at the pulley on the right,
F = 0
F = 2 T - 40 N - 200 N = 0
2 T = 240 N
T = 120 N
S = 40 N + 2 T = 40 N + 2 (120 N)
S = 280 N
D6.5 A cable and pulley arrangement is shown here. The coefficient of friction between the two blocks is 0.4. The coefficient of friction between the block and the floor is 0.4. What is the maximum external horizontal force F that can be exerted on the lower block before it will move? What is the tension in the cable?
The maximum external force F that can be exerted will be the force exerted when the friction forces are at their maxima,
Ff = µ FN Make careful free body diagrams of the forces on each block.
First, for the 2-kg block, we have
F = 0
But that really means
With the normal force on the 2 kg block known, we can readily calculate the friction force,
Fx = 0
and Fy = 0
Fx = Ff - T = 0
Fy = FN - 20 N = 0
Ff = T FN = 20 N Ff = (0.4) (20 N)
Ff = 8 NAnd that also means
T = 8 N Now, look at all the forces on the 7-kg block,
The downward 20 N-force on top of the block is the normal force exerted by the 2-kg block. The 8-N force on the top is the friction force exerted by the 2-kg block. The tension is still 8 N just as it was at the other end of the string which is attached to the 2-kg block. The forces labeled FN and Ff are the normal force and friction force exerted at the bottom on this 7-kg block, of course. We used the same symbols to represent different forces earlier when we looked at the 2-kg block. Now we are ready to again apply the first condition of equilibrium,
F = 0
But that really means
Fx = 0
and Fy = 0
Fx = F - Ff - 8 N - 8 N = 0
Fy = FN - 20 N - 70 N = 0
F = Ff + 16 N FN = 90 N With the normal force on the 7-kg block known, we can readily calculate the friction force,
Ff = (0.4) (90 N)
Ff = 36 N
F = Ff + 16 N
F = 36 N + 16 N
F = 52 N
(Circular Motion)
D6.6 A horse moves with a tangential speed of 1.9 m/s when it is 8.5 m from the center of a carousel. Calculate its centripetal acceleration. If a 70-kg person sits on the horse, what is the net force on the rider?
ac = v2/r = = 0.42 m/s2
Fc = m ( v2/r ) = ( 70 kg ) ( 0.42 m/s2 ) = 29.7 N
D6.7 A coin sits 15.0 cm from the center of a variable-speed turntable. The coin remains in place as the speed of the turntable increases until it reaches a rate of 2 revolutions per second and then it starts to slide. What is the coefficient of friction between the coin and the surface?
First, find the linear speed coin and its centripetal accleration.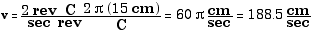
To have this acceleration, the net force must be
Fnet = Fc = m v2/r = m (23.7 m/s2) Since we do not know the mass of the coin, we will put into the equation simply as “m” and expect that it will later “drop out”.
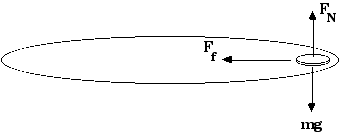
Now apply
F = m a
Fy = m ay
and Fx = m ax
Fy = FN - mg = 0
- Ff = - m v2 / r
FN = mg Ff = µ FN - µ FN = - m v2 / r µ FN = m v2 / r µ mg = m v2 / r µ g = v 2 / r µ = v 2 / g r µ = (188.5 cm/s)2 / [(980 cm/s2)(15 cm)] µ = 2.41 µ = 2.41 is a fairly large coefficient of friction; that is, there must be rubber or something like that on the bottom of the coin.
D6.8 A 1200-kg car makes a curve on a flat road of radius 60 m at a speed of 15 m/s. Will the car be able to make the turn if
a) the pavement is dry and has a coefficient of friction of 0.65?
b) there is oil on the pavement and the coefficient of friction is only 0.20?
The free body diagram for this looks much like the free body diagram for problem D6.7 above.
The friction force must provide the centripetal acceleration. Being on a flat curve, the normal force happens to equal the weight; FN = m g .
Now applyF = m a
Fy = m ay
and Fx = m ax
Fy = FN - mg = 0
- Ff = - m v2 / r
FN = mg - µ FN = - m v2 / r
µ FN = m v2 / r
µ mg = m v2 / r µ g = v2 / r µ = v2 / g r
µ = (15 m/s)2 / [(9.80 m/s2)(60 m)]
µ = 0.38 µ = 0.38 is the minimum value of the coefficient of friction that is necessary to provide enough friction force to equal the centripetal force required to allow the car to make the curve.
Therefore, . . .a) Yes, the car can make the curve when µ =0.65.
b) No, the car will not make the curve when µ = 0.20.
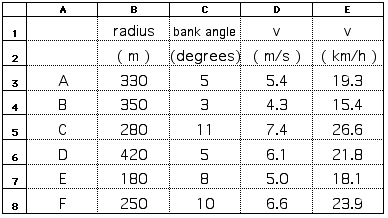
D6.9 The table below lists data for six banked highway curves-giving the radius of each curve and the angle at which the curve is banked. Find the maximum speed at which these curves may be traveled without depending upon friction and rank them from slowest to fastest
Curve: A B C D E F radius 330 m 350 m 280 m 420 m 180 m 250 m bank angle 5° 3° 11° 5° 8° 10° For calculations that are going to be repeated, it is best to solve the problem symbolically once and then plug particular values into the resulting solution. A spreadsheet is a convenient way to carry out this final calculation.
We already knowtan = v2 / r
or
v2 = r tan 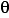
D6.10 A 60-kg pilot comes out of a dive by flying along an arc of radius 800 m with a speed at the bottom of 120 km/h. What is her apparent weight?
v = 120 km/hr [1000 m/km] [hr/3600 s] = 33.3 m/s
Fnet = FN - m g = m v2 / r
FN = m g + m v2 / r
FN = m ( g + v2 / r )
FN = (60 kg) [ (9.8 + {(33.3)2 / 800 m }) m/s2 ]
FN = (60 kg) [ (9.8 + 1.4) m/s2 ]
FN = (60 kg) [ 11.2 m/s2 ]
FN = 672 N
D6.11 A car of mass 1000 kg goes over the crest of a hill whose radius of curvature is 40 m measured in a vertical plane.
(a) What is the force of the car on the road surface if the car’s speed is 15 m/s?
(b) Calculate the magnitude and direction of the necessary force between car and road if the speed at the top of the crest is 20 m/s. Explain your answer.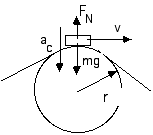
Fnet = m g - FN = m v2/r = Fc
FN = m g - m v2/r
FN = m [ g - v2/r ]
a) v = 15 m/sFN = (1000 kg) [ (9.8 m/s2) - ]
FN = (1000 kg) [ 9.8 - 5.6 ] m/s2
FN = (1000 kg) [4.2 ] m/s2
FN = 4,200 N = 4.2 kN
b) v = 20 m/sFN = (1000 kg) [ (9.8 m/s2) - (20 m/s)2/(40 m)]
FN = (1000 kg) [ 9.8 - 10 ] m/s2
FN = (1000 kg) [ - 0.2 ] m/s2
FN = - 200 N
Of course, the road can not exert a negative (meaning downward) normal force. Therefore, the car looses contact with the road!
D6.12 In the ROTOR ride on a midway, passengers are pressed against the inside vertical wall of a rotating drum 2.5 m in radius. This drum takes 2.0 seconds to make a complete rotation; that is, it rotates at 30 rpm (revolutions/minute).
(Six Flags - St Louis has this ride and there it is known as "Tom's Twister". Take a look at it next summer -- as participant or as observer!)
(a) Viewed from an Earth-based frame of reference outside the drum, what are the magnitude and direction of the force of the wall on a rider whose mass is 70 kg?
Initially the rider’s weight is supported by the floor. After the ROTOR is at full speed the floor is removed.
(b) If the coefficient of static friction between the passenger and the wall is 0.6, will the passenger slip or be held pressed against the vertical wall?
(c) Describe the situations -- including the forces -- from the reference frame of the passenger.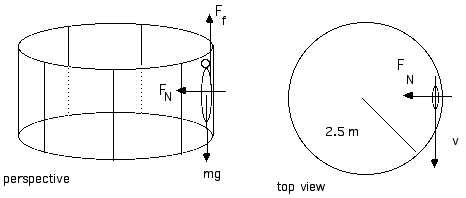
The normal force, FN, provides the centripetal force, Fc = m v2 / r.
v = =
=
= 7.8 m/s
FN = Fc = m
= (70 kg)
= 1,730 N
For comparison, the rider’s weight is
w = mg = (70 kg)(9.8 m/s2) = 686 N so the normal force is about two and a half times as large. The normal force is directed inward, toward the center of the circle.
Now the floor of the ROTOR is moved down and the friction force, pointing up, must equal the weight, pointing down, to keep the rider from sliding down along with the floor.
The maximum value of the friction force isFf,max = µ FN = (0.6) (1,730 N) = 1,040 N The maximum friction force is greater than the weight. Therefore, the actual friction force will just equal the weight and the passenger will remain in place on the wall of the ROTOR.
From inside the ROTOR, from the noninertial reference frame, the passenger will feel pushed to the outside by a “centrifugal force” to which the wall responds with the normal force. Because there is a normal force, there can be a friction force and all the rest is the same.
| ToC, Chapter 6 | Course Calendar |
(c) 2005, Doug Davis; all rights reserved
| ToC, Chapter 6 | Course Calendar |
![]()
(c) 2005, Doug Davis; all rights reserved