PHY 1151

Doug Davis

Ch 2, One-Dimensional Kinematics:

Questions Only

Everything will come from our "Big Three Kinetmatics Equations":

D2.1 A bicyclist travels with an average velocity of 15 km/h, North for 20 minutes. What is his displacement?

D2.2 The speed of sound in air is about 330 m/s. You observe a lightning bolt strike a tree 1.5 km away. How much time will elapse between your seeing the lightning bolt and hearing the thunder that accompanies it? Why do you not need to take into account the speed of light?

D2.3 A car accelerates from rest to 90 km/h in 8.8 s. What is its average acceleration in m/s²?

D2.4 A jet aircraft landing on an aircraft carrier is brought to a complete stop (v_f = 0) from a (an initial) velocity of (v_i= ) 215 km/h in 2.7 seconds. What is its average acceleration in m/s²?

D2.5 A certain car has an acceleration of 2.4 m/s². Assume that its acceleration remains constant. Starting from rest, how long does the car require to reach a velocity of 90 km/h? How far does it travel while reaching that velocity?

D2.6 In passing a slow truck you must accelerate from 50 km/h to 90 km/h. What must your acceleration be so you can complete your passing maneuver in 1.0 km?

D2.7 A car, speeding at 130 km/h passes a police car at rest. Just as the speeding motorist passes the police car, the police car begins pursuit. If the police car maintains a constant acceleration of 5.8 m/s², when and where will the speeding motorist be overtaken?

D2.8 A late commuter, sprinting at 8 m/s, is 30 m away from the rear door of a commuter train when it starts to pull out of the station with an acceleration of 1 m/s². Can the commuter catch the train (if the platform is long enough)?

D2.9 While standing still, a police car is passed by a speeding car traveling at a constant 120 km/h. The policeman waits 2 seconds before deciding to pursue. What must be his acceleration in order to catch the speeding car within three kilometers?

D2.10 How fast must a stone be thrown, straight up, to just reach the top of a building that is 10 m high?

D2.11 Cliff divers in Acapulco dive from rocks about 35 m above the water. Neglecting air resistance, what is their velocity as they hit the water?

D2.12 In the mid-1960’s McGill University, in Montreal, launched high-altitude weather sensors by firing them from a cannon made from two World War II Navy cannon bolted together for a total length of 18 m. It was proposed that they use this arrangement to launch a satellite. Orbital speed of a satellite is about 29 000 km/h. What would have been the average acceleration throughout the 18 m length of the cannon to have a muzzle velocity of 29 000 km/h?

D2.13 A falling flower pot takes 0.25 s to pass by a window 1.5 m high. How far above the top of the window was the balcony from which the flower pot fell?

D2.14 Poor Wyl E Coyote is at it again. Attempting to catch the Road Runner he falls from the top of a 400 m cliff. He is wearing an Acme Fireworks rocket but requires 6 seconds to light the fuse and ignite the rocket. The burning rocket gives him an upward acceleration so that his velocity just reaches zero as he reaches the bottom.

a) How far has he fallen before the rocket starts?

b) What is his upward acceleration in order to have this gentle landing?

But, alas, as Edsel Murphy would have it, the Acme rocket does not shut off. Nor is the Coyote able to release himself from the rocket. Therefore, the rocket now carries him upward with this same acceleration for an additional 5 seconds before it depletes its fuel.

c) How high is he then (as the fuel runs out)?

d) How fast is he moving then?

e) How high -- how far above the canyon floor -- does the Coyote eventually go?

f) How fast is he going as he hits the canyon floor this time?

2.15 The figure below is a position-time graph for a lab cart traveling along a straight track in a Physics lab. Determine the time(s) that the cart

a) has its greatest velocity.

b) has constant velocity.

c) is moving backward.

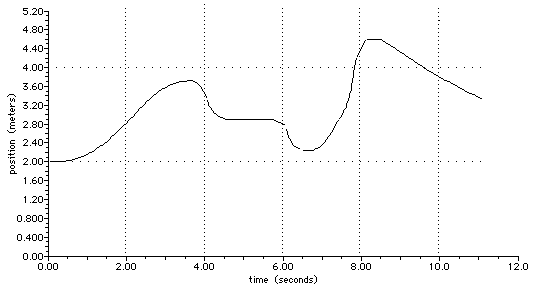
D2.16 The Figure below is a position-time graph. From it construct the corresponding velocity-time and acceleration-time graph. (That is, do not worry about the acceleration-time graph as the data given is really not sufficient).

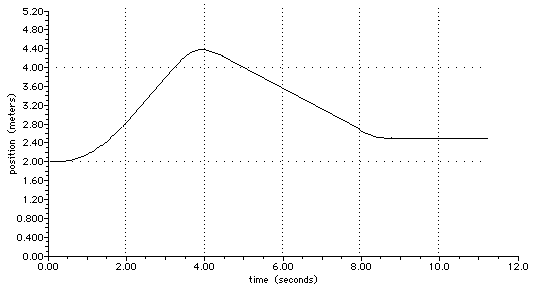
D2.17 The Figure below is an acceleration-time graph. Use it to construct corresponding position-time and velocity-time graphs. Start the car from rest, vi = 0, at x = 0 for t = 0.

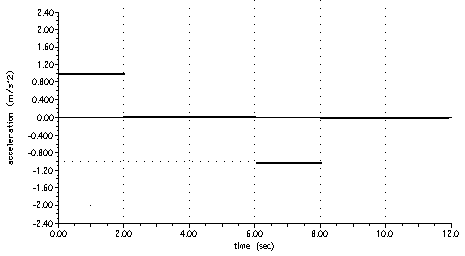
D2.17 (second version!) The figure below is an acceleration-time graph. Use it to construct the corresponding position-time and velocity-time graphs. Start the car (or whatever) from rest, vi = 0, at x = 0 for t = 0.

 

| ToC, Chapter 2 | Course Calendar |

 

(c) 2005, Doug Davis; all rights reserved