
PHY 1151
Doug Davis

PHY 1151
Doug Davis
![]()
| ToC, Chapter 1 | Course Calendar |
![]()
D1.5. A tabletop measures 4 ft by 5 ft. What is the area of the tabletop in square meters?A = l w A = (4 ft) (5 ft) = 20 ft2
A = 20 ft2 [(12 in / 1 ft) (2.54 cm / 1 in) (1 m / 100 cm)]2
A = 1.86 m2
Or, as an alternative method, we could change the lengths first and then multiply,
l = 4 ft (12 in / 1 ft) (2.54 cm / 1 in) (1 m / 100 cm) = 1.22 m w = 5 ft (12 in / 1 ft) (2.54 cm / 1 in) (1 m / 100 cm) = 1.52 m
A = l w
A = (1.22 m) (1.52 m)
A = 1.86 m2
D1.12. Express 65 mi/h in kilometers per hour.v = 65 (mi/h) (1.61 km/mi) v = 105 km/h
D1.19. Being careful to give the answer to the appropriate number of significant figures, add the following numbers: 29.34, 35.452, 123.92, and 8.934 .If we just plug these numbers into a calculator, like
we will get an answer of 197.646. However, we do not know all the numbers to the same accuracy. It may help to re-write this addition with the unknown parts shown explicityl, like
Now we can see that the answer is really just 197.64 .
This answer, for addition, is only good -- or significant -- for the number of decimal places beyond the decimal point as the smallest number of decimal places beyond the decimal point in the numbers that are being added.
D1.23. The length of a card is measured as 42.3 cm; its width, as 12.764 cm. To the correct number of significant figures, what is the area of the card?A = l w Again, if we just enter the numbers into a calculator, we get
A = (42.3 cm) (12.764 cm) = 539.9172 cm2 However, for multiplication (and division), the number of significant figures in the answer is equal to the smallest (or smaller) number of significant figures in the factors that are being multiplied. The length, 42.3 cm, is known only to three significant figures so that determines the number of significant figures in the answer. Since we have 539.9172 cm2 when we round that to three significant figures we get 540 cm2 .
A = 540 cm2
D1.33. Light from a helium-neon laser has a wavelength of 632.8 nm. Express this in meters, using scientific notation.wavelength = 632.8 nm [ 1 x 10 - 9 m / nm ] = 632.8 x 10 - 9 m wavelength = 6.328 x 10 - 7 m
D1.34. Add the following numbers, being careful to keep only the appropriate significnt figures in your answer: 9.135 x 102, 3.375 x 104, 1.934 x 103.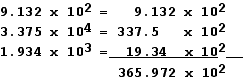
But, as before, it may help to explicitly show what digits are unknown,
365.9 x 102
D1.41. A mechanical watch is advertised as not gaining or losing more than 5 s a month. What is the percent accuracy of this watch? That is, if it gains (or loses) 5 s in a 30-cay month, how accurate -- expressed as a percentage -- is the time it reads?Inaccuracy = uncertainty / number Inaccuracy = (5 s) / (1 mo)
1 mo = 1 mo (30 da/1 mo) (24 h/1 da) (60 min/1 h) (60 s/1 min)
1 mo = 2 592 000 s = 2.592 x 106 s
Inaccuracy = (5 s) / (2.592 x 106 s)
Inaccuracy = 1.9 x 10 - 6
Inaccuracy = 1.9 x 10 - 6 (100%)
Inaccuracy = 1.9 x10 - 4 %
Inaccuracy = 0.000 19 %
Accuracy = 100% - Inaccuracy
Accuracy = 100 % = 0.000 19 %
Accuracy = 99.999 81 %
| ToC, Chapter 1 | Course Calendar |
![]()
(c) 2005, Doug Davis; all rights reserved