PHYsics 1151

Exam 3

November 14, 2005

| Calendar Page | Old Exams |

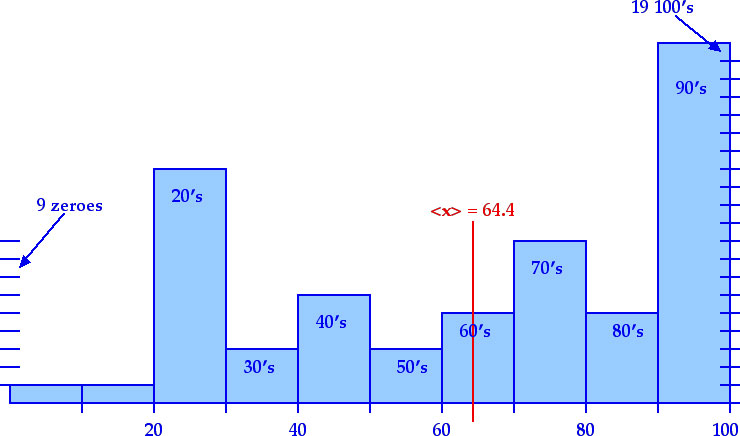
Comments from my soapbox: With thirty-nine scores of 90% and above, including nineteen 100's, this was clearly an easy test! However, there were also nine zeroes! That's terrible. The "equation sheets" you make out should help with anxiety or increase confidence. The "equation sheets" do not provide an alternative to understanding the material -- understanding the ideas and principles involved! This is a three-hour course; it is still probably impossible to survive the course with less than six hours a week in homework and study outside of class. Homework remains vital to surviving the course! All the questions on Exam 3 had come directly from the homework (Exam 2 was all "new" questions that I wrote without consulting previous notes). Be prepared. Read the textbook (that's the single best source). Work the homework! Study previous exams. Study the worked examples in the textbook.

| Calendar Page | Old Exams |

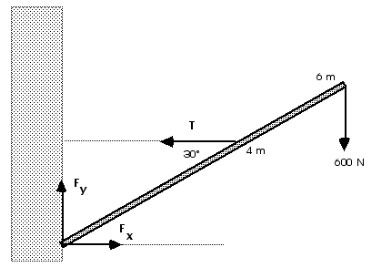
1. A lightweight, uniform pole is 6 m long and is attached by a pivot at one end to a wall. The pole is held at an angle of 30° above the horizontal by a horizontal guy wire attached to the pole 4.0 m from the end attached to the wall. A load of 600 N hangs from the upper end of the pole. Find the tension in the guy wire and the components of the force exerted on the pole by the wall.

From the first condition of equilibrium, we have

F = 0

But that really means

Fx = 0
and
Fy = 0
Fx = Fx - T = 0

Fy = Fy - 600 N = 0
Fx = T

Fy = 600 N

[ The vector nature of forces is important. There is no way you should ever be adding Fx and Fy as scalar components. That makes no sense at all! ]

[ The weight of an object, the force of gravity down on some mass, is w = mg. The mass m will be measured in kg and the weight, in N (newtons). This is a lightweight boom and no mass was given. Its mass is negligible. The load of 600 N already is a force. Mupliplying 600 N by 9.8 m/s2 is meaningless! ]

More information is needed to solve for T and Fx. We can get that information from the second condition of equilibrium. Before we start to calculate torques, we must decide on the reference point about which we will calculate those torques. If we choose the lower, left end of the pole, there are two forces, Fx and Fy, that will have zero torque. That will reduce the number of terms in all of our equations. Therefore, that is a good choice for the origin or reference point or axis of rotation.

List each force and the torque caused by that force:

Fx: = 0 (since r = 0 in = r F sin )
Fy: = 0 (since r = 0 in = r F sin )
T: ccw = (4 m)(T)(sin 30°) = (4 m) T (0.50) = (2 m) T
600 N: cw = (6 m)(600 N)(sin 60°) = (6 m)(600 N)(0.866) = 3118 m-N

ccw means a counter clockwise torque and cw means a clockwise torque.

ccw = cw
(2 m) T = 3118 m-N
T = 1559 N

[ Be careful with your arithmetic; several of you correctly wrote (2 m) T = 3118 m-N and then divided both sides of the equation by (2 m) and -- somehow -- found T = 1159 N. Calculators are wonderful. But they still work under the rule of GIGO: Garbage In, Garbage Out. A calculator is a useful tool; but make sure it's just a tool. You're still in charge! ]

Therefore,

Fx = T

Fx = 1559 N

And we already knew

Fy = 600 N

2. Calculate the mass of Jupiter, given that its moon Callisto has a mean orbital radius of 1.88 x 106 km and an orbital period of 16 days, 16.54 hours.

The force of gravity provides the centripetal force to keep Callisto in its orbit.

Fg = G MJ m / r2 = m v2 / r = Fc
MJ =

We must find the linear speed of Callisto.

v =

T = 16 d, 16.54 h = [(16)(24) + 16.54 ] h = 400.54 h
T = 400.54 h [3600 s/h] = 1.44 x 106 s

Fgravity = Fcentripetal

Fgravity = G MJ mC/r2 = mC v2/r = Fcentripetal

G MJ mC/r2 = mC v2/r

MJ = r v2/G


MJ = 1.9 x 1027 kg

The acceleration of gravity at Earth's surface, g = 9.8 m/s2, has nothing to do with this problem!

3. An object undergoes simple harmonic motion with an amplitude of 12 cm. At a point 8.0 cm from equilibrium, its speed is 20 cm/s. What is the period?

Caution: be very careful with the units!

We have used lower case m for both mass and meters. That gets confusing here so I will go to upper case M for mass.

E = PE max = (1/2) k A2

A = 12 cm = 0.12 m
E = (1/2) ( k ) (0.12 m)2
E = KE + PE = (1/2) M v2 + (1/2) k x2
E = (1/2) M (0.2 m/s)2 + (1/2) k (0.08 m)2 = (1/2) ( k ) (0.12 m)2 = E
M (0.2 m/s)2 = k (0.12 m)2 - k (0.08 m)2
M (0.2 m/s)2 = k [ (0.12 m)2 - (0.08 m)2 ]
(M/k)(0.2 m/s)2 = (0.12 m)2 - (0.08 m)2
(M/k)(0.04) (m/s)2 = (0.12 m)2 - (0.08 m)2
(M/k)(0.04) (m/s)2 = (0.0144 - 0.0064) m2
(M/k)(0.04) (m/s)2 = (0.0144 - 0.0064) m2 = 0.0080 m2
(M/k)(0.04) (m/s)2 = 0.0080 m2
(M/k)(0.04) (m/s)2 = 0.0080 m2 / [ (0.04) (m/s)2 ]
(M/k) = 0.2 ( s2 )
T = 2 SQRT(M/k)
T = 2.8 sec

4. A guitar string 0.70 m long is tuned to play A at 440 Hz whe its full length vibrates. Where should a finger be placed in order to play C at 524 Hz?

The velocity of the wave on the string is given by

v = f
/2 = 0.70 m
= 1.4 m
v = (440 Hz) (1.4 m)
v = 616 m/s

/2 = 0.588 m


That is, your finger should be placed so the string that vibrates is 0.588 m (or 0.59 m) long.

[The guitar string is only 0.70 m long. So any answer with a length greater than that makes no sense!]

5. A hydraulic lift supports a car that weighs 1.2 x 104 N. The diameter of the piston connected to the pump is d1 = 2.0 cm. The diameter of the piston supporting the car is d2 = 10.0 cm. What force must the pump exert on its piston to lift or support the car?
Remember, A = π r2 ; r = d/2 .

Because the areas are different, the forces will be [quite] different. But the pressures are the same (if the two pistons are at the same height),

F2 = W = weight of the car = 1.2 x 104 N

Hydraulic lifts are used so a pump can provide a small force which the hydraulic lift "amplifies" to lift the car. If you calculate a force for the pump that is greater than the weight of the car, something went wrong! Always ask if your answer is plausible, reasonable, expected, or if it makes any sense at all.

| Calendar Page | Old Exams |