Physics 1151
Exam #3
November 15, 2002
Possibly useful equations:
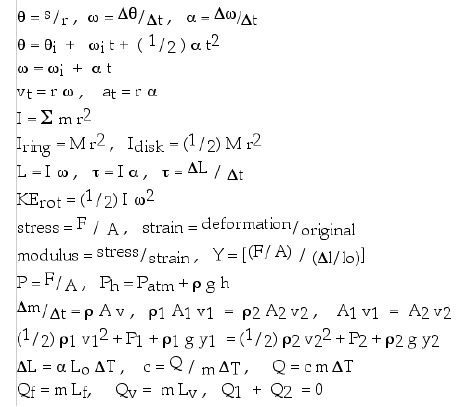
My powers of intuition and guessing are non-existent. Please make your answers clear and easy to follow. Unlabeled numbers make it very difficult to guess or figure out what you are doing. Tell me the details! Label and explain what you are doing.
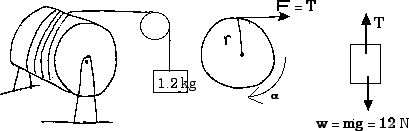
1. (9.29) A solid, uniform
cylinder of 12 cm radius with mass of 5.0 kg is free to rotate about its symmetry
axis. A cord is wound around the drum and a 1.2 kg mass is attached to the end
of the cord. Find the acceleration of the hanging mass, the angular acceleration
of the cylinder, and the tension in the cord.
For the 1.2 kg mass, take down as positive and apply Newton's Second Law,
Fnet = m a
Fnet = 12 N - T = (1.2 kg) a
12 N - T = (1.2 kg) a
For the rotating cylinder, apply the rotational form of Newton's Second Law,
net = I 
net
= r F sin 
net = (0.12
m) (T) (1)
since = 90°
For a solid cylinder,
I = (1/2) M r2
I = (0.5) (5.0 kg) (0.12 m)2
I = 0.036 kg m2
Therefore,
net = (0.12
m) T = (0.036 kg m2)
At the moment, we have three unknowns, T, a, and ,
in two equations. The angular acceleration of the cylinder and the linear acceleration
of the cord or of the hanging mass are connected by
a = r
a = (0.12 m)
= a / 0.12 m
(0.12 m) T = (0.036 kg m2)
(0.12 m) T = (0.036 kg m2) [ a / 0.12 m]
T = (0.036 kg m2) a/[ (0.12 m)2(0.12 m) ]
T = (0.036 kg m2) a/(0.12 m)2
T = (2.5 kg) a
Now we have two equations in two unknowns
12 N - T = (1.2 kg) a
12 N - (2.5 kg) a = (1.2 kg) a
12 N - (2.5 kg) a = (1.2 kg) a
12 N = (3.7 kg) a
a = 12 N / 3.2 kg
a = 3.24 m/s2
T = 8.1 N
2. (10.56) What percentage of a copper cube floats above the surface if it floats in mercury?
(Hg)
= 13,600 kg/m3
(Cu)
= 8,920 kg/m3
v2 + g h
+ p = constant
v12 +
g h1 + p1 = 1/2
v22 +
g h2 + p2
(0)2 + g
(0) + p1g = 1/2
(0)2 + g
(12 m) + (0) g
(12 m)4. (12.57) A 0.050-kg ice cube, initially at – 5.0°C, is placed in 0.30 kg of water at 25°C.
What is the final temperature of the water?
Or, if melting is not complete, how much ice remains unmelted at thermal equilibrium?
Assume no heat is lost to the environment.
First, assume all the ice melts, so Tf > 0°C
Q1 + Q2 = 0
Q1 = heat lost by the water
Q1 = cwater mwater
Twater
= (4186 J/kg C°)(0.30 kg)(Tf – 25°C)
Q1 = (4186 J/kg C°)(0.30 kg)(Tf
– 25°C) = 1,256 (J/C°) Tf –
31,395 J
Q2 = heat gained by ice
Q2 = heat gained in raising ice to 0°C +
+ heat gained in melting ice +
+ heat gained in raising the melted ice (now water) to temperature Tf
Q2 = cice mice T1
+ Lf,ice mice + cwater mice DT2
Q2 = [2090 J/kg C°][0.05 kg][0°C –
(– 5°C)] +
+ [3.33 x 105 J/kg][0.05 kg] +
+ [4186 J/kg C°][0.05 kg][Tf – 0°C]
Be very careful with these temperature changes !
Q2 = 522.5 J + 16,650 J + 209.3 (J/C°)
Tf – 0
Q2 = 17,172.5 J + 209.3 (J/C°) Tf
Now we are ready to go back to
Q1 + Q2 = 0
1,256 (J/C°) Tf – 31,395 J + 17,172.5
J + 209.3 (J/C°) Tf = 0
1,256 (J/C°) Tf + 209.3 (J/C°)
Tf = 31,395 J – 17,172.5 J
1,465 (J/C°) Tf = 14,222 J
Tf = [14,222/1,465]°C
Tf = 9.7°C
5. Concept Questions:
i) Consider a twirlling ice skater (or a dizzy Physics professor) who spends
faster as she (or he) pulls her (or his) hands in close. Spinning increases
because angular momentum is conserved. However, the rotational kinetic
energy increases. This increase in kinetic energy means
that work was done. Where or how is work done in this situation to increase
the kinetic energy?
An inward force is required to pull the weights inward. That force is supplied
by the arms of the rotating skater (or professor) and acts through a distance
so that provides the work done to increase the kinetic energy.
ii) Consider an ocean liner that leaves l’Harve, France, crosses
the Atlantic Ocean, enters the St Lawerence River, and docks at Montreal, Quebec.
The Atlantic Ocean is sea water and the St Lawerence is fresh water. What happens
to the draft of the ocean liner as it goes from the salt water of the
Atlantic to the fresh water of the St Lawerence? Why? The “draft”
of a ship is the depth of the ship below the water.
The bouyant force must equal the weight of the vessel. The bouyant force
is provided by the weight of the water displaced. Since sea water has a greater
density, less sea water must be displaced. That means the draft in fresh water
will be greater (deeper) than the draft in sea water.
iii) In class, I demonstrated a ping-pong ball in a funnel. As I blew
air through the funnel, the ping-pong ball was held in place.
Why? Why was it not blown out of the funnel?
The Bernoulli effect is that moving air exerts less pressure than
still air. The moving air between the funnel and the ping-pong ball exerts less
pressure than the still air on the other side of the ping-pong ball. The greater
pressure on the other side of the ping-pong ball means there is greater force
there, pushing the ball into the funnel.
iv) Name a thermometric property and describe how it can be used
in a thermometer?
A thermometric property is a property that changes with the temperature.
As a liquid is heated, its volume expands. This can be used
to make a common liquid-in-glass thermometer.
As a metal is heated, its length increases. This can be used to make a bimetallic
strip thermometer.
As a resistor is heated, its resistance changes. This can be used to make an
electronic thermometer.
As a gas is heated, its volume expands. This can be used to make a constant
volume gas thermometer. We used such a thermometer to come up with the absolute
temperature scale, now more usually known as the Kelvin temperature scale.