

First Hour Exam
February 4, 2000
![]()
Possibly useful information:
s = si + vi t + (1/2) a t2v = vi + a t
v2 = vi2 + 2 a (s - si)
sin q = opp/hyp
cos q = adj/hyp
tan q = opp/adj
F = m a
F12 = - F12
fs,max = µs n
fk = µk n
g = 9.8 m/s2
10 m/s2
Statistics:
High:
100
Mean:
48
Low:
6
| Return to PHY 1150's Home Page |

1. A car starts from rest and accelerates at a constant 4.2 m/s2.
a) How far has it gone when its speed is 35 m/s?b) Convert 35 m/s to a speed in units of km/h.
v2 = vi2 + 2 a (s - si) (35 m/s)2 = (0)2 + 2(4.2 m/s2)(s - 0)
(35 m/s)2 = (0)2 + 2(4.2 m/s2)(s - 0)
1225 m2/s2 = (8.4 m/s2) s
s = (1225 m2/s2) / (8.4 m/s2)
s = 145.8 m
v = 35 m/s
v = 35 m/s [ 1 km/1000 m ][ 3600 s/1 h]
v = 126 km/h
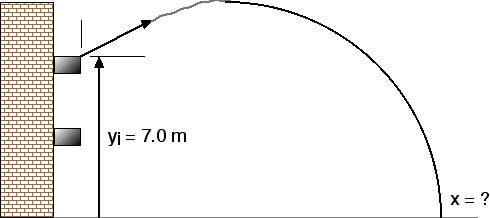
2. A ball is thrown from a third-floor balcony, 7.0 m above the parking lot below. The ball is thrown with an initial velocity of 10 m/s, at an angle of 37° above the horizontal.
a) What are the horizontal and vertical components of its initial velocity?b) How long is the ball in the air, before it strikes the parking lot below?
c) How far from the building does it strike the parking lot below?
a) What are the horizontal and vertical components of its initial velocity?
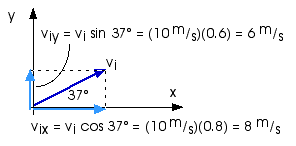
vix = vi cos 37° = (10 m/s)(0.8) = 8 m/s
viy = vi sin 37° = (10 m/s)(0.6) = 6 m/s
b) How long is the ball in the air, before it strikes the parking lot below?
s = si + vi t + (1/2) a t2 y = yi + viy t + (1/2) ay t2
y = yi + viy t + (1/2) ( - g) t2
0 = 7 m + (6 m/s) t + (1/2) ( - 10 m/s /s ) t2
0 = 7 + 6 t - 5 t2
5 t2 - 6 t - 7 = 0
This is a quadratic equation, like
a x2 + b x + c with
a = 5, b = - 6, and c = - 7
We are only interested in t > 0, so we have only
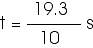
t = 1.93 s
c) How far from the building does it strike the parking lot below?
While it is in the air, its horizontal velocity remains constant,
vx = vix = 8 m/s = const x = vx t
x = (8 m/s ) (1.93 s)
x = 15.4 m
3. Add the following vectors:
A = 3 i + 4 j
B = 5 i - 6 j
C = 7 i - 8 j
A = 3 i + 4 j
B = 5 i - 6 j
C = 7 i - 8 j
R = A + B + C
a) Write the resultant R in i, j-notation.
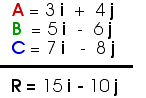
b) Make a reasonable sketch of R.
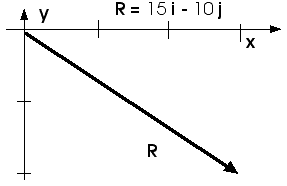
c) Find the magnitude and direction of R.
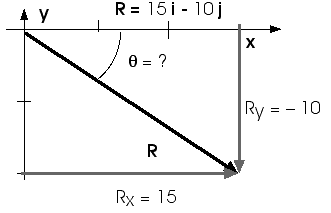
R = 18
|

4. A 2 kg block sits on a smooth (frictionless) plane inclined 20° above the horizontal. It is connected by a string to a 5 kg mass that hangs suspened from the other end of the string as shown in the sketch above.
a) Draw clear, complete "free-body" diagrams showing all the forces on the two masses.b) Apply Newton’s Second Law, F = m a, to the two masses and find the acceleration of the system.
a) Draw clear, complete "free-body" diagrams showing all the forces on the two masses.
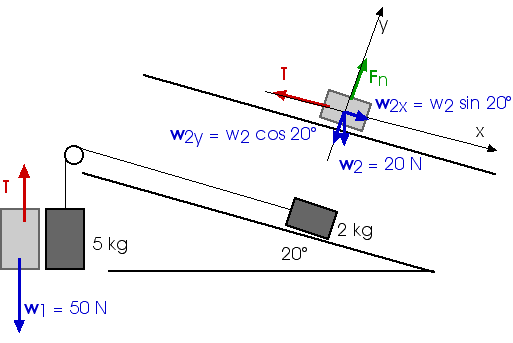
b) Apply Newton's Second Law, F = m a, to the two masses and find the acceleration of the system.
First, look at the 5-kg, hanging mass. Since we "expect" this mass to accelerate downward, we will take "down" as positive here.
Fnet = w1 - T = m1 a w1 - T = (5 kg) a
50 N - T = (5 kg) a
This is one equation with two unknowns. That means we need more information so we turn to the forces on the 2 kg block on the plane.
Fnet,y = FN - wy = m2 ay FN - wy = 0
FN - w cos 20o = 0
FN - 0.94 w = 0
FN = 0.94 w
FN = 0.94 (20 N)
FN = 18.8 N
This may be "interesting" but we don't really need to know the normal force for this problem with the frictionless plane. Look at the forces in the direction along the plane. I have labeled this direction as the x-direction. Since we have assumed the 5-kg hanging block will accelerate downward, we likewise assume this 2-kg block on the plane accelerates along the negative x-axis so we take that direction as positive.
Fnet,x = m2 ax Fnet,x = T - wx
T - wx = m2 ax
T - w sin 20o = (2 kg) ax
T - (20 N) (0.34) = (2 kg) ax
T - 6.8 N = (2 kg) ax
This is another single equation with two unknowns. But the two accelerations are the same. The 2-kg block is attached by a string to the 5-kg block so the hanging block accelerates with the same acceleration as the 2-kg block accelerates along the inclined plane. That is, ax = a. Solve for the tension T in one of the equations and use that expression in the other equation.
50 N - T = (5 kg) a T = 50 N - (5 kg) a
Now use that in
T - 6.8 N = (2 kg) a [ 50 N - (5 kg) a ] - 6.8 N = (2 kg) a
50 N - (5 kg) a - 6.8 N = (2 kg) a
43.2 N = (2 kg) a + (5 kg) a
43.2 N = (7 kg) a
a = [ 43.2 / 7 ] [ N / kg ]
a = [6.2] [ N / kg ] [ (kg-m/s2) / N ]
a = 6.2 m/s2
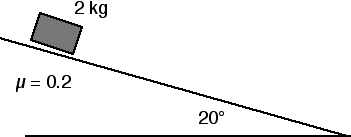
5. A 2-kg block slides down a plane inclined at 20° from the horizontal as shown in the diagram above. The coefficient of sliding friction between the block and the plane is µ = 0.2.
a) Make a good, clear, complete "free-body diagram" showing all the forces on the 2-kg mass.b) Apply Newton’s Second Law, F = m a, to the mass and find the acceleration of the block down the inclined plane.
c) How fast will the block be moving when it has traveled 1.0 m down the plane?
a) Make a good, clear, complete "free-body diagram" showing all the forces on the 2-kg mass.
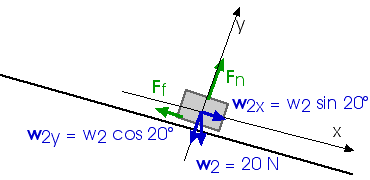
b) Apply Newton's Second Law, F = m a, to the mass and find the acceleration of the block down the inclined plane.
While we usually say or write
F = m a we must always remember that F is the net force, Fnet
Fnet = m a and that this is a vecor equation so it is really elegant shorthand notation for
Fnet,x = m ax and Fnet,y = m ay Fnet,x = wx - Ff Fnet,y = FN - wy wx - Ff = m ax FN - wy = m ay = 0 w sin 20o - Ff = m ax FN = wy 0.34 w - Ff = m ax FN = w cos 20o 0.34 (20 N) - Ff = m ax FN = 0.94 w 6.8 N - Ff = (2 kg) ax FN = 0.94 (20 N) Ff = FN
FN = 18.8 N Ff = (0.2)(18.8 N) Ff = 3.8 N 6.8 N - 3.8 N = (2 kg) ax 3.0 N = (2 kg) ax ax = 1.5 m/s2 c) How fast will the block be moving when it has traveled 1.0 m down the plane?
v2 = vi2 + 2 a (s - si) v2 = 02 + 2 (1.5 m/s2) (1.0 m)
v2 = 3.0 m2/s2
v = 1.73 m/s
| Return to PHY 1150's Home Page |