
Bernoulli's Equation
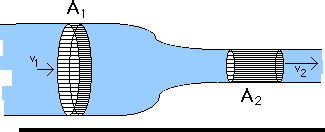
From the Equation of Contunity,
we know that the fluid must be moving slower at position 1 where the cross section A1 is larger and it must be moving faster at position 2 where cross section A2 is smaller. That is, the fluid must accelerate as is moves from position 1 to position 2. That means the pressure on the fluid at position 1 must be greater than the pressure at position 2 in order to provide a net force to cause this acceleration. This is an example of Bernoulli's Principle that
the pressure exerted by a moving fluid is greater where the speed of the fluid is smaller and the pressure is smaller where the speed of the fluid is greater.
Now consider fluid that flows -- along a stream tube -- with a change in cross sectional area and a change in height. Work must be done on the fluid to change its kinetic energy and its potential energy.
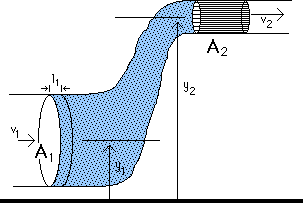
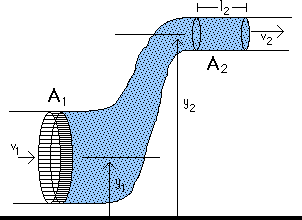
At position 1, the force on the shaded portion of the fluid is
Likewise, at position 2,
The work done at the two positions is
and
Gravity also does work,
where
so that
We know that the net work on anything equals the change in kinetic energy,
W1 + W2 + Wgrav = (1/2) m v22 - (1/2) m v12
P1 A1 l1 - P2 A2 l2 - m g (y2 - y1) = (1/2) m v22 - (1/2) m v12
(1/2) m v12 + P1 A1 l1 + m g y1 = (1/2) m v22 + P2 A2 l2 + m g y2
(1/2) ![]() 1
A1 l1 v12 +
P1 A1 l1 +
1
A1 l1 v12 +
P1 A1 l1 + ![]() 1
A1 l1 g y1 =
1
A1 l1 g y1 =
= (1/2) ![]() 2
A2 l2 v22 +
P2 A2 l2 +
2
A2 l2 v22 +
P2 A2 l2 + ![]() 2
A2 l2 g y2
2
A2 l2 g y2
Recall that
(1/2) ![]() 1
V v12 + P1 V +
1
V v12 + P1 V + ![]() 1
V g y1 = (1/2)
1
V g y1 = (1/2) ![]() 2
V v22 + P2 V+
2
V v22 + P2 V+ ![]() 2
V g y2
2
V g y2
(1/2) ![]() 1
v12 + P1 +
1
v12 + P1 + ![]() 1
g y1 = (1/2)
1
g y1 = (1/2) ![]() 2
v22 + P2 +
2
v22 + P2 + ![]() 2
g y2
2
g y2
This means
or
If the vertical height y does not change, this means
or
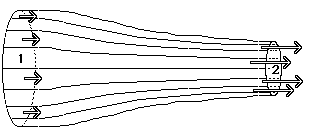
Venturi tube or venturi flow meter:

 Click here
for another Example.
Click here
for another Example.
|
|
|
|
|
|
|
|
||
|
|
|||