Simple Harmonic Motion
Motion that repeats itself is periodic
motion. A particular kind of periodic motion is known as simple
harmonic motion. When an object is disturbed from equilibrium, its
motion is probably simple harmonic motion. Here are some examples
of periodic motion that approximate simple harmonic
motion:
A particular and useful kind of
periodic motion is simple harmonic motion (SHM). Our prototype for
SHM is a mass attached to a spring.
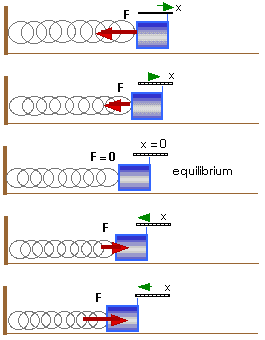
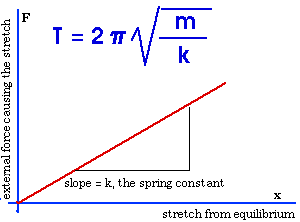
For this spring-and-mass simple harmonic
oscillator, we find the period is given by
The restoring force exerted by the
spring is F = - kx,
F = - kx
So the net force on our Simple
Harmonic Oscillator (SHO) is
Fnet = - k x =
ma
or
a = - (k/m) x
for our prototypical
SHO.
The amplitude is the maximum
distance the mass moves from its equilibrium position. It moves as
far on one side as it does on the other.
The time that it takes to make one
complete repetition or cycle is called the period of the
motion. We will usually measure the period in seconds.
Frequency is the number of cycles
per second that an oscillator goes through. Frequency is measured in
"hertz" which means cycles per second.
Period and frequency are
closely connected; they contain the same information.
T = 1/f
f = 1/T
The position of this prototypical SHO can
be written as
x(t) = A sin (2
f t)
In discussing SHM, 2
f occurs so often that we give it a special symbol and
name,
2
f = 
This is the lower case Greek letter
"omega" and it is called the angular frequency. f is
the frequency , measured in cycles per second or hertz (Hz)
while
is the angular frequency, measured in radians per
second.
Of course, if the position x(t) does not
start at zero when the time t starts at zero, the equation
above,
x(t) = A sin (2
f t)
will have (or cause) problems! We can
handle this change in time by writing this as
x(t) = A sin (2
f t + 
)
is the lower case Greek letter "phi" and is usually called the "phase
angle" or the "phase shift". It is simply related to where the SHO is
when time t is zero.
In terms of the angular frequency
,
we can write the equation for the position of a SHO as
x(t) = A sin (
t)
or
x(t) = A sin (
t + )
An interesting and important
characteristic of all simple harmonic motion is that the period
remains the same even for motions with quite different
amplitudes.
Circular motion is another
example of motion whose period is independent of the amplitude.
Two riders on a merry-go-round have the same period even tho' one
sits near the edge and has a large amplitude while the other sits
near the axis of rotation and has a small amplitude.
(c) 2005, Doug Davis; all rights reserved
