
Torque ( "Rotational Force" )
Remember, torque is a vector. When we write
or
![]()
r and F are vectors and their "cross product" or "vector product" is also a vector! We determine the direction of the "cross product" or "vector product" by the "right hand rule".
![]()
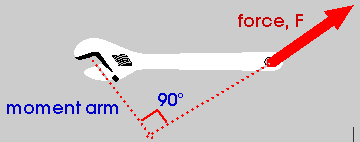
The perpendicular distance from the axis of rotation (or pivot) to the "line of action" of the force F is called the "moment arm" (sometime, the "lever arm").
Draw a vector r from the axis of rotation to the location of the force F.
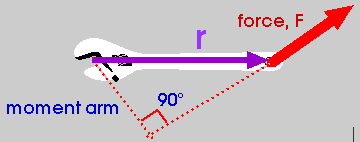
To evaluate a cross product such as
![]() we must redraw the vectors r and F so
they begin at a common origin:
we must redraw the vectors r and F so
they begin at a common origin:

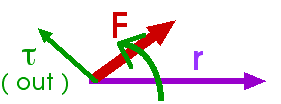
Now rotate the first
vector, r, into the second vector,
F, using the fingers of your right hand (!). The new
vector, tau ![]() ,
now points in the direction of your thumb!
,
now points in the direction of your thumb!
The order is important in a "cross product" or a "vector product".
D = B x A
C = - D
A x B = - B x A
The "cross product" or "vector product" does not commute!
|
|
|
|
|
|
|
|
||
|
|
|||