
Rotational Forces: Torques
A rotational force, also known as a torque, depends upon the force and where that force is applied;
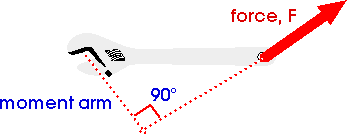
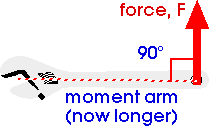
The lever arm is the perpendicular distance from the force to the axis of rotation.
Consider the torque exerted on this wrench by a force applied in different directions or in different places.

 |
Consider the rotational force -- or the torque -- acting on a door when you try to open it by exerting a force in various places or in various directions. |
|
|
We can write this aswhere
is the "moment arm" or the "lever arm", the perpendicular distance from the origin to the line of action of the force.
We can also write this as
where
is the component of the force perpendicular to the line (the position vector r) drawn from the origin to the point of application of the force.
Furthermore, we can also write this as
where
is the angle between r and F.
This can also be written as
where we have now used the cross product or the vector product. If we have two vectors A and B, we may define the cross product or the vector product by

and
We will return to this vector nature of the rotational force, or torque, later.
For now, we simply have four different ways of writing the same thing.


ToC Rotation Torque 2 Return ToC, Static Equilibrium (c) 2002, Doug Davis; all rights reserved