

Strings & Springs
This same idea and technique can be used is slightly different situation,
Example: Consider a lamp hanging from a chain. What is the tension in the chain?
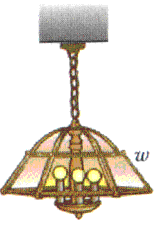
As always, begin with a "free body diagram". Tension T acts upward on the lamp while the force of gravity pulls down with force w, the weight of the lamp. The net force is the vector sum of these two forces. The lamp is not accelerating so the force up must equal the force down. In terms of magnitudes, this means
T = w
Tension: Tension is the magnitude of the force exerted by a chain or a rope or a string. The direction of that force depends upon the rest of the situation and the object that we are concentrating on at the moment. If we concentrate on the chain shown below, the downward force T' is the force exerted on the chain by the lamp while the upward force T'' is the force exerted on the chain by the ceiling. There is no substitute for good free-body diagrams.
Springs exert forces as they are stretched and compressed. First, we need to know about the general characteristics of a spring.
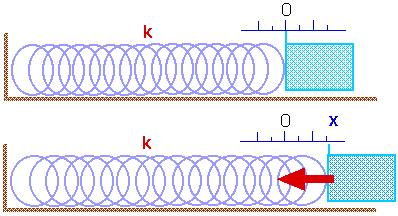
Experimentally, we find the force exerted by a spring is proportional to the distance it has been stretched or compressed. Of course, the force exerted by the spring is equal and opposite to the external force exerted on the spring to cause it to stretch or to be compressed.
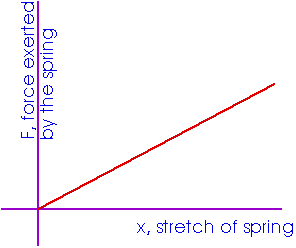
This is known as Hooke's law
We might write this in equation form as F = k x. However, the force exerted by the spring is always in the opposite direction to the stretch (or compression) of the spring. This proportanity is known asHooke's law and can be written as
F = - k x This is the force exerted by the spring. The external force we exert on the spring is Fext = + k x.
The proportionality constant k is known as the spring constant and describes how stiff the spring is. This


(c) Doug Davis, 2005; all rights reserved