Uniform Circular Motion

Consider an object moving along a circular path with constant or uniform speed. This might be a guest on a carousel at an amusement park, a child on a merry-go-round at a playground, a car with a lost driver navigating a round-about or "rotary", a yo-yo on the end of a string, a satellite in a circular orbit around Earth, or Earth in a (nearly) circular orbit around our Sun.

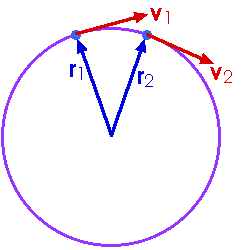
As an object travels in a circle, the direction of its velocity changes. Even tho' the speed remains uniform, the velocity changes because its direction changes.

v = v₂ - v₁

This is not zero, even tho'

| v₂ | = v₂ = | v₁ | = v₁ = v

v is the speed, which remains constant. You can see v from the following diagram:

Notice the two similar triangles in the position vectors and the velocity vectors,

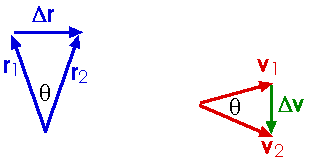
or

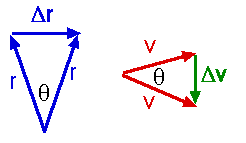
or

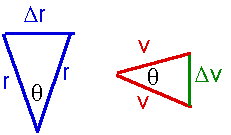
Since these are similar triangles,we know that

v / v = r / r

For small changes in time or for small angles , the distance r is very nearly given by

r = v t

This means

v / v = r / r

v / v = v t / r

v = v²t / r

v /t = v² / r

v /t is the acceleration an object has because it moves in a circle; this is called the centripetal acceleration a_c and is directed toward the center of the circle. That is,

a_c = v² / r

---

Angular velocity

How fast is something turning or rotating or revolving? We call this its angular velocity and give it the symbol , the lower case Greek letter omega. It may have units of revolutions per minute or revolutions per second or, better yet, radian per second.

Most of us are comfortable measuring an angle in degrees. But measuring an angle in radians is usually more useful.

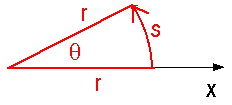
While we can measure the angle in degrees using a protractor, there is another way to measure or define this angle . This -- or any other -- angle can be defined as the ratio of the arc length s to the radius r; that is,

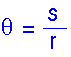
Such a definition means this measure of the angle has no dimensions. We have taken an arc length, measured in something like meters, and divided it by a radius, also measured in something like meters. However, since we expect dimensions or units, we call this unit of angular measure a radian. You may think of radians as added for cosmetic purposes! How large is a radian?

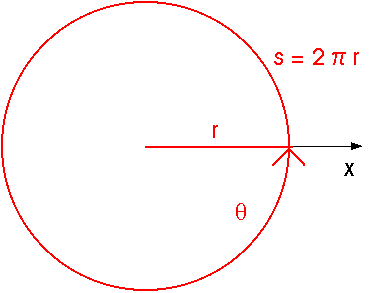
Consider a complete circle. We would describe a complete circle as having an angle of 360^o. In terms of radians, a complete circle has an arc length equal to its circumference, s = C = 2 r.

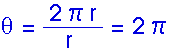
What does all this have to do with uniform circular motion? The arc length traveled by a point on a rotating object is equal to the radius of that point multiplied by the angle through which it has rotated,

s = r

when is measured in radians

That means the linear speed v of a point on a rotating object is equal to the radius of that point multiplied by the angular speed with which it is rotating, provided is measured in radians per time. That is,

v = r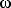

provided is measured in radians per time (as in radians per second).

Example

An audio CD rotates at 150 rpm (revolutions per minute). What is the linear speed of a small scratch on the CD that is 10 cm from the center?

v = r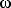

v = (10 cm) (150 ^rev/_min) [ 2 ^rad /_rev ] [ ^min/ _{60 s} ]

v = 157 cm / s

Projectile Motion			Accelerations
Return to ToC, 2D Motion

(c) 2005, Doug Davis; all rights reserved