

Displacement, Velocity, and Acceleration
Much of what we have developed for One-Dimensional Motion can be immediately extended to vector notation for Two-Dimensional Motion.
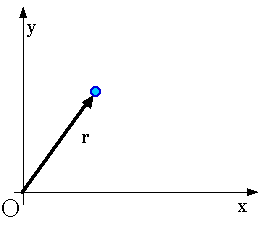
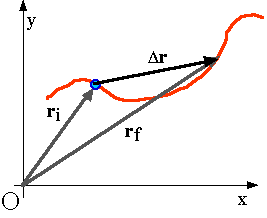
DisplacementThe location of an object is given by the displacement vector that locates an object relative to some origin.
VelocityAs an object changes its position, we will want to describe how fast it is moving. As with one-dimensional motion, we will define the average velocity as the ratio of the change in its displacement to the change in time to which that corresponds,
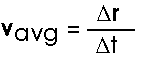
Notice that the velocity and the displacement are vectors. We are no longer limited to a change in displacement along a straight line.
r is a vector.
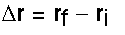
As with one-dimensional motion, we often want to know about the instantaneous velocity, the velocity at this moment. That is the average velocity over a smaller and smaller time interval. As before, this instantaneous velocity is often called simpley "the velocity".
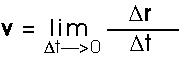
This limit process, of course, means the velocity is the time derivative of the displacement.
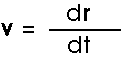
Remember, velocity v and displacement r are both vectors.
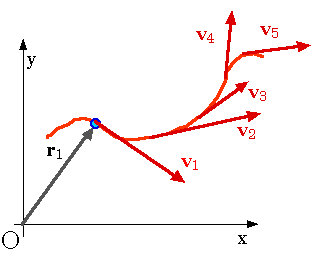
Notice that the velocity vector is tangent to a particle's path.
AccelerationOf course, we will want to ask how fast the velocity is changing. Just as earlier, this is the acceleration,
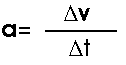
This is really the average acceleration and we can go to the instantaneous acceleration by using ever smaller time intervals
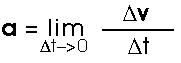
The vector acceleration a is the time derivative of the vector velocity. As before, we will usually say "the acceleration" when we mean "the instantaneous acceleration".


Unit Vectors Summary Return to ToC, Vectors (c) 2005, Doug Davis; all rights reserved