

Vector Properties

Two vectors a and b are equal if they have the same direction and the same magnitude (or length). We could then write
a = b
A vector a may be multiplied by a scalar s (remember, a scalar is an ordinary number). We could write this new vector as
c = s a This new vector c has the same direction as vector a and its magnitude is s times the magnitude of a.
We write the magnitude (or length) of a vector without boldface or without a vector over it. The magnitude of a vector is an ordinary scalar; there is no direction associated with the magnitude of a vector.
Speed is the magnitude of velocity and distance is the magnitude of displacement.
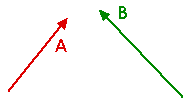
Consider two vectors A and B which we want to add. They might be displacement vectors or velocity vectors or electric field vectors -- or any vectors at all. We can add them graphically by drawing vector A and then, at the tip of vector A, drawing vector B as shown below. The sum of vectors is called the resultant. The resultant vector R, is the vector that we can draw from the beginning of A to the end of B. We can write this as
R = A + B
Vector addition is commutative. That means the order in which we add vectors does not affect the resultant. To add vectors A and B we could begin by drawing vector B. At the end of vector B we would then draw vector A. The resultant vector R is then the vector we can draw by starting at the beginning of B and finishing at the end of A. We could write this as
R = B + A These resultants are exactly the same. That means
A + B = B + A
Sometime people will draw the vectors in twice to form a parallelogram as shown below. The resultant R is the diagonal as shown. This is referred to as vector addition by the parallelogram method.
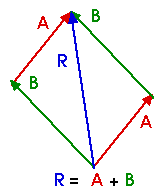
My favorite description of vector addition involves the pieces of an ancient treasure map. Suppose we find these fragments or pieces of an old treasure map. "the old oak tree" becomes the origin of our coordinate system.

Each of these pieces of the map -- each of these statments of distance and direction -- may be represented by a vector:

If we follow these directions in this order, we walk along the route given by
R = A + B + C + D The resultant vector R locates where we end up after following these directions in this order. As we will see, this resultant is
R = 11.2 paces at 27o west of north.
But the pieces of the treasure map may be shuffled. That is, we may follow the directions in a different order. Here is a vector addition diagram for
R = B + C + D + A We still end up at the same spot. The resultant is independent of the order in which we add the vectors.
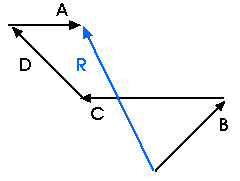
We might shuffle the pieces of the treasure map yet again and follow their directions in still a different order. Here is a vector addition diagram for
R = B + A + D + C
For these three examples, and all the other possible permutations, the resultant R will always be the same. To determine R we can carefully construct one of these drawings to scale and then carefully measure the length of R and the direction of R. When we do this we will find
R = 11.2 paces at 27o west of north


Vectors and Scalars Components Return to ToC, Vectors and 2D Motion (c) 2005, Doug Davis; all rights reserved