Excursions in Physics

Homework, Chapter 4: Newton's Laws of Motion

Ex 4, 6, 11, 21, 22, 27, 31, 34, 36, 43; Pb 2, 3, 5

Exercises (Discussion Questions)

Ex 4.4 In tearing a paper towel or plastic bag from a roll, why is a quick, sharp jerk more effective than a long, slow pull?

A quick, sharp jerk means a greater acceleration and a greater acceleration means a greater force. And it is force that tears the paper towel or plastic bag.

Ex 4.6 Before the time of Galileo and Newton, it was thought by many learned scholars that a stone dropped from the top of a tall mast of a moving ship would fall vertically and hit the deck behind the mast by a distance equal to how far the ship had moved forward while the stone was falling. In light of your understanding of Newton's Laws, what do you think about this?

As we have seen on The Mechanical Video, and as I have tried to demonstrate in walking back and forth in front of the classroom while throwing a ball, the ball or stone should fall and hit the deck at the base of the mast.

Ex 4.11 What is your own mass in kilograms? Your weight in newtons?

Recall that the a mass of 1 kg has a weight of 2.2 lbs. To find mass in kilograms, take your weight in lbs and divide by 2.2 (this means a weight of 2.2 lbs corresponds to a mass of 1.0 lbs or a weight of 22 lbs corresponds to a mass of 10 kg or a weight of 220 lbs corresponds to a mass of 100 kg.)

Recall that the weight of 1 kg is 9.8 newtons. To find your weight in newtons, take your mass in kilograms and multiply by 9.8 .

Here is a short table:

Ex 4.21 Nellie Newton hangs at rest from the ends of the rope as shown. How does the reading on the scale compare to her weight?

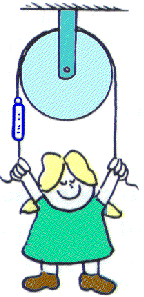
There are two forces pulling her up -- the force exerted by each rope on each hand. Those two forces are balanced by her own weight. So the force exerted by the rope is one-half her weight. The force exerted by the rope is called the tension in the rope.

Ex 4.22 Harry the painter swings year after year from his bosun's chair. His weight is 500 N and the rope, unknown to him, has a breaking point of 300 N. Why doesn't the rope break when he is supported as shown here with both ends of the rope attached to his bosun's chair?

One day Harry is painting near a flagpole, and, for a change, he ties the free end of the rope to the flagpole instead of to his chair, as shown here. Why did Harry end up taking his vacation early?

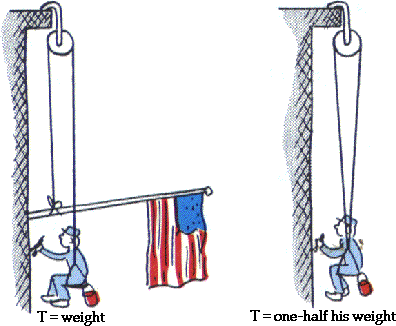
In his usual method of hanging from the bosun's chair (shown on the right), the rope pulls up on Harry with two forces so each force is only one-half Harry's weight, and that is only 250 N. But in the sketch on the left, with one end of the rope attached to the flagpole, the rope pulls up with only one force so that must be equal to all of Harry's weight, and that is 500 N. But, before that happens, the rope breaks (and Harry falls!).

Ex 4.27 Two 100 N weights are attached to a spring scale as shown. Does the scale read 0, 100, or 200 N, or give some other reading?

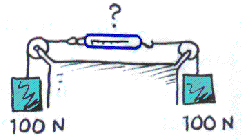
Each string exerts a force of 100 N to suspend the hanging mass to which it is attached. This means the tension in the string is 100 N. So the scale will read 100 N.

Ex 4. 31 What is the net force on an apple that weighs 1 N when you hold it at rest above the floor? What is the net force on it when you release it?

For anything at rest, the net force is zero.

When you release the apple, the only force on it is the force of gravity, which we call the weight of the apple, and we are told that that is one Newton.

Ex 4.34 Why can you exert greater force on the pedals of a bicycle if you pull up on the handlebars?

As you pull up on the handlebars of the bicycle, they exert a force down on you which you can pass along to the pedals.

Ex 4.36 Suppose two carts, one twice as massive as the other, fly apart when the compressed spring that joins them is released. How fast does the heavier cart roll compared to the lighter cart?

The forces on the two cart will be the same (but in opposite directions). The heavier cart will have one-half the acceleration of the lighter one since it has twice as much mass.

Ex 4.43 How does the weight of a falling body compare to the air resistance it encounters just before it reaches terminal velocity? After?

Before reaching terminal velocity, the falling body is still accelerating, so its weight (the force of gravity) is still greater than the force due to air resistance.

After reaching terminal velocity, the falling body falls with constant speed so the net force on it must be zero. This means the force of gravity (its weight) acting downward is just balanced by the force of air resistance acting upward.

Pb 4.2 If a mass of 1 kg is accelerated 1 m/s² by a force of 1 N, what would be the acceleration of 2 kg acted on by a force of 2 N?

Use Newton's Second Law,

Pb 4.2 How much acceleration does a 747 jumbo jet of mass 30 000 kg experience in takeoff when the thrust of each of four engines is 30 000 N (for a total thrust of 120 000 N)?

Again, use Newton's Second Law,

Pb 4.3 If you stand next to a wall on a frictionless skateboard and push the wall with a force of 30 N, how hard does the wall push you? If your mass is 60 kg, what is your acceleration?

From Newton's Third Law, the Law of Action and Reaction, we know that the wall also pushes on you with a force of 30 N. Now we again use Newton's Second Law,

Pb 4.5 A firefighter of mass 50 kg slides down a vertical pole with an acceleration of 5 m/s². What frictional force does the pole exert on her?

First, we can find the net force, for that is always the F that appears in Newton's Second Law,

What forces make up this net force F_net? Gravity pulls down with the firefighter's weight,

Then there is the force of friction, F_f, which opposes her motion. So the force of friction F_f must point up. The net force F_net is made up of these two forces,

Ex 4.(***extra***) Can a dog wag its tail without the tail in turn "wagging the dog"? Explain. (Consider a dog with a relatively massive tail.)

Newton's Third Law tells us that the tail will exert a force on the dog as the dog exerts a force on the tail. Therefore the tail will also "wag the dog".

Typical multiple-guess questions:

1. Newton's First Law of Motion states that, in the absence of a net force, an object in motion will

a) eventually come to rest

b) continue in motion but slow down until it stops

c) continue in motion with the same speed along the same straight line

d) continue along the same straight line with a decrease in speed

2. Mass is a measure of

a) the volume of an object

b) the size of an object

c) how difficult it is to change the motion of an object

d) the velocity of an object

3. The weight of an object is

a) the same thing as the mass of an object

b) the sum of all the forces on an object

c) the force of gravity on an object

d) always less than the mass, even in a vacuum

4. The net force on a 1-kg object, at rest, is

a) 9.8 N

b) 4.9 N

c) 1.00 N

d) zero

5. The net force on a 1-kg object, in free fallt, is

a) 9.8 N

b) 4.9 N

c) 1.00 N

d) zero

6. Harry the Painter has a weight of 500 N. When he is suspended as shown in the sketch here, what is the tension in the rope?

a) 1000 N

b) 500 N

c) 250 N

d) 25 N

7. A force of 24 N acts on an object whose mass is 6 kg. This causes the object to accelerate at

a) 2 m/s²

b) 4 m/^s2

c) 6 m/s²

d) 10 m/s²

8. A car, with mass of 1,000 kg, accelerates at 2 m/s². The net force exerted on the car must be

a) 500 N

b) 1,000 N

c) 2,000 N

d) 10,000 N

9. The weight of a 1,000-kg car is

a) 500 N

b) 1,000 N

c) 2,000 N

d) 10,000 N

10. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 3 m/s2. The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be

a) 90 N

b) 150 N

c) 350 N

d) 500 N

1. Newton's First Law of Motion states that, in the absence of a net force, an object in motion will

a) eventually come to rest

b) continue in motion but slow down until it stops

c) continue in motion with the same speed along the same straight line

d) continue along the same straight line with a decrease in speed

2. Mass is a measure of

a) the volume of an object

b) the size of an object

c) how difficult it is to change the motion of an object

d) the velocity of an object

3. The weight of an object is

a) the same thing as the mass of an object

b) the sum of all the forces on an object

c) the force of gravity on an object

d) always less than the mass, even in a vacuum

4. The net force on a 1-kg object, at rest, is

a) 9.8 N

b) 4.9 N

c) 1.00 N

d) zero

5. The net force on a 1-kg object, in free fallt, is

a) 9.8 N

b) 4.9 N

c) 1.00 N

d) zero

6. Harry the Painter has a weight of 500 N. When he is suspended as shown in the sketch here, what is the tension in the rope?

a) 1000 N

b) 500 N

c) 250 N

d) 25 N

Gravity pulls down on the painter with his weight, 500 N. The rope pulls up on the painter twice with those forces being equal to the tension in the rope. Since the painter isn't moving, the sum of the forces up must balance the force down. Each end of the rope pulls up with a tension of 250 N.

7. A force of 24 N acts on an object whose mass is 6 kg. This causes the object to accelerate at

a) 2 m/s²

b) 4 m/s²

c) 6 m/s²

d) 10 m/s²

F = m a

24 N = ( 6 kg ) ( a )

24 N = ( 6 kg ) ( 4 m/s²)

a = 4 m/s²

8. A car, with mass of 1,000 kg, accelerates at 2 m/s². The net force exerted on the car must be

a) 500 N

b) 1,000 N

c) 2,000 N

d) 10,000 N

9. The weight of a 1,000-kg car is

a) 500 N

b) 1,000 N

c) 2,000 N

d) 10,000 N

w = mg

w = (1,000 kg) (10 m/s²)

w = 10,000 N

10. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 3 m/s². The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be

a) 90 N

b) 150 N

c) 350 N

d) 500 N

F = ma

F_net = ma

F_net = F_gravity - F_frict

F_gravity = w = m g

500 N = m (10 m/s²)

m = 50 kg

F_net = ma = (50 kg) (3 m/s²)

F_net = 150 (kg m/s²)

F_net = 150 N

F_net = F_gravity - F_frict

150 N = 500 N - F_frict

F_frict = 500 N - 150 N = 350 N

F_frict = 350 N