PHY 1150
Chapter 13; Oscillations about Equilibrium

| Return to Calendar |

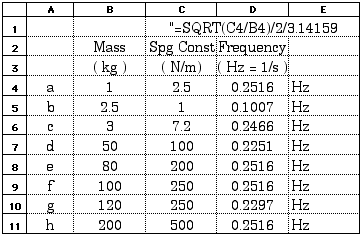
D13.1 Find the frequency of a mass on a spring oscillator with the following values for the mass and the spring constant:
mass (kg)
spring constant ( N / m )

a
1.0
2.5
b
2.5
1.0
c
3.0
7.2
d
50
100
e
80
200
f
100
250
g
120
250
h
200
500

This is an excellent one to solve with a spreadsheet:

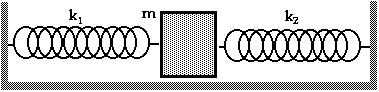
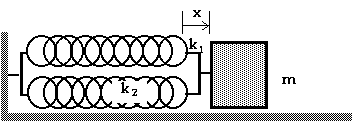
D13.2 Find the frequency of the oscillator in this arrangement with the mass attached between two springs of spring constants k 1 and k 2.

 

The next arrangement of springs is a little more "tricky" or more interesting. Find the frequency of the oscillator in this arrangement with the mass attached to two springs of spring constants k 1 and k 2 as shown in the diagram here.

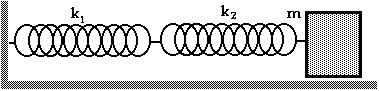
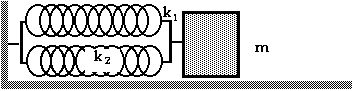
And with this third arrangement, again, find the frequency of the oscillator with the mass attached to two springs of spring constants k 1 and k 2 as shown in the diagram here.

For any simple harmonic oscillator, we have

where k in this equation is the "effective spring constant", the spring constant of a single spring that has the same effect as the combination of springs in the diagram.

With this arrangement, a displacement of x causes a force of F1 = - k 1 x due to the spring on the left and a force of F2 = - k 2 x due to the spring on the right.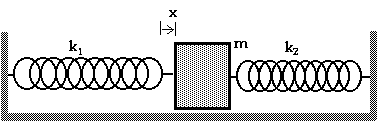

The net force, then, is Fnet = F1 + F2 = - k 1 x - k 2 x = - (k 1 + k 2)x. Since the effective spring constant, keff is the constant is Fnet = - k eff x, we can see that

k eff = k 1 + k 2

The next arrangement of springs is a little more "tricky" or more interesting:

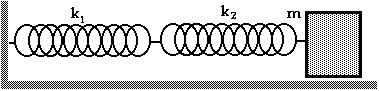
When the mass is moved a distance x, spring #1 stretches a distance x 1 and spring #2 stretches a distance x 2 with

x = x 1 + x 2

That is, the two springs need not be stretched (or compressed) the same amount at all. However, the force exerted by each spring must be the same. That is,

F1 = F2

or

k 1 x 1 = k 2 x 2

or

x1 = ( k 2 / k 1 ) x 2

or

x 2 = ( k 1 / k 2 ) x 1

To determine the "effective spring constant", we must write the force in the form of

F = - k eff x

We have

F = - k 1 x 1

and

x = x 1 + x 2
x = x 1 + ( k 1 / k 2 ) x 1
x = [ 1 + ( k 1 / k 2 )] x 1

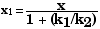
Therefore,

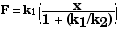
Therefore,

which can also be written as

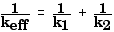
The third arrangement of springs is actually fairly easy and straightforward. With this arrangement, a displacement of x causes a force of F1 = - k1x due to spring #1 and a force of F2 = - k2x due to spring #2. The stretch of each spring is the same as the displacement of the mass.

The net force, then, is Fnet = F1 + F2 = - k 1 x - k 2 x = - ( k 1 + k 2 ) x. Since the effective spring constant, k eff is the constant is Fnet = - k eff x , we can see that

k eff = k 1 + k 2

D13.3 How much work is done when a spring with spring constant 80 N/m is stretched 0.15 m (or 15 cm)?
W = (1/2) k x2
W = (1/2) (80 N/m) (0.15 m)2
W = 0.9 J

D13.4 Consider, as a simple harmonic oscillator, a 200 g (0.20 kg) mass attached to spring with a spring constant of 50 N/m. If the oscillator has an amplitude of 10 cm (0.1 m), what is the maximum speed of the mass?
W = PE = (1/2) k A2 = (1/2) (50 N/m) (0.1 m)2 = 0.25 J

As the mass moves through equilibrium,

x = 0

so it has zero potential energy and its total energy is now all KE,

KE = (1/2) m v 2 = (1/2) (0.2 kg) v 2 = 0.25 J = E
v2 = 2.5 m 2 / s 2
v = 1.58 m / s

D13.5 An object undergoes simple harmonic motion with an amplitude of 12 cm. At a point 8.0 cm from equilibrium, its speed is 20 cm/s. What is the period?

Caution: be very careful with the units!

We have used lower case m for both mass and meters. That gets confusing here so I will go to upper case M for mass.

E = PE max = (1/2) k A2

A = 12 cm = 0.12 m
E = (1/2) ( k ) (0.12 m)2
E = KE + PE = (1/2) M v2 + (1/2) k x2
E = (1/2) M (0.2 m/s)2 + (1/2) k (0.08 m)2 = (1/2) ( k ) (0.12 m)2 = E
M (0.2 m/s)2 = k (0.12 m)2 - k (0.08 m)2
(M/k)(0.2 m/s)2 = (0.12 m)2 - (0.08 m)2
(M/k)(0.04) (m/s)2 = (0.0144 - 0.0064) m2 = 0.0080 m2
(M/k) = 0.2 ( s2 )
T = 2 SQRT(M/k)
T = 2.8 sec

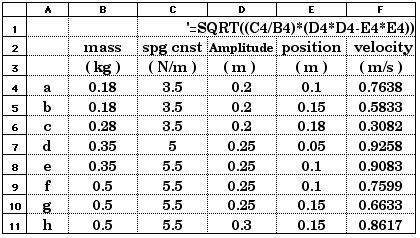
D13.6 For each of the simple harmonic oscillators listed in the table below, find the velocity of the mass at the position given:

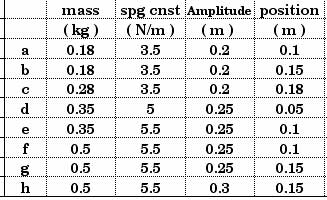
These multiple-data-set problems are good ones to solve with a spreadsheet. This is basically energy conservation,

E = (1/2) k A2 = (1/2) k x2 + (1/2) m v2
k A2 = k x2 + m v2
m v2 = k (A2 - x2)
v2 = (m/k) (A2 - x2)

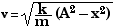
So this will be the formula we put in the spreadsheet:

D13.7 A 50-g (0.050 kg) mass hanging from a spring oscillates with a frequency of 2 Hz. What is the spring constant?

f 2 = ( 1/2 ) 2 (k/m)
f 2 = ( 1/4 2)(k/m)
k = 4 2 f 2 m
k = 4 2 [2 (1/s )] 2 (0.050 kg)
k = 3.95 kg/s2
k = 3.95 N/m

| Return to Calendar |

(c) 2005, Doug Davis; all rights reserved